nLab Introduction to Topology -- 1
This page contains a detailed introduction to basic topology. Starting from scratch (required background is just a basic concept of sets), and amplifying motivation from analysis, it first develops standard point-set topology (topological spaces). In passing, some basics of category theory make an informal appearance, used to transparently summarize some conceptually important aspects of the theory, such as initial and final topologies and the reflection into Hausdorff and sober topological spaces. We close with discussion of the basics of topological manifolds and differentiable manifolds, hence of differential topology, laying the foundations for differential geometry.
main page: Introduction to Topology
this chapter: Introduction to Topology 1 – Point-set topology
next chapter: Introduction to Topology 2 – Basic Homotopy Theory
For introduction to more general and abstract homotopy theory see instead at Introduction to Homotopy Theory.
Context
Topology
topology (point-set topology, point-free topology)
see also differential topology, algebraic topology, functional analysis and topological homotopy theory
Basic concepts
-
fiber space, space attachment
Extra stuff, structure, properties
-
Kolmogorov space, Hausdorff space, regular space, normal space
-
sequentially compact, countably compact, locally compact, sigma-compact, paracompact, countably paracompact, strongly compact
Examples
Basic statements
-
closed subspaces of compact Hausdorff spaces are equivalently compact subspaces
-
open subspaces of compact Hausdorff spaces are locally compact
-
compact spaces equivalently have converging subnet of every net
-
continuous metric space valued function on compact metric space is uniformly continuous
-
paracompact Hausdorff spaces equivalently admit subordinate partitions of unity
-
injective proper maps to locally compact spaces are equivalently the closed embeddings
-
locally compact and second-countable spaces are sigma-compact
Theorems
Analysis Theorems
Point-set Topology
The idea of topology is to study “spaces” with “continuous functions” between them. Specifically one considers functions between sets (whence “point-set topology”, see below) such that there is a concept for what it means that these functions depend continuously on their arguments, in that their values do not “jump”. Such a concept of continuity is familiar from analysis on metric spaces, (recalled below) but the definition in topology generalizes this analytic concept and renders it more foundational, generalizing the concept of metric spaces to that of topological spaces. (def. below).
Hence, topology is the study of the category whose objects are topological spaces, and whose morphisms are continuous functions (see also remark below). This category is much more flexible than that of metric spaces, for example it admits the construction of arbitrary quotients and intersections of spaces. Accordingly, topology underlies or informs many and diverse areas of mathematics, such as functional analysis, operator algebra, manifold/scheme theory, hence algebraic geometry and differential geometry, and the study of topological groups, topological vector spaces, local rings, etc. Not the least, it gives rise to the field of homotopy theory, where one considers also continuous deformations of continuous functions themselves (“homotopies”). Topology itself has many branches, such as low-dimensional topology or topological domain theory.
A popular imagery for the concept of a continuous function is provided by deformations of elastic physical bodies, which may be deformed by stretching them without tearing. The canonical illustration is a continuous bijective function from the torus to the surface of a coffee mug, which maps half of the torus to the handle of the coffee mug, and continuously deforms parts of the other half in order to form the actual cup. Since the inverse function to this function is itself continuous, the torus and the coffee mug, both regarded as topological spaces, are “the same” for the purposes of topology; one says they are homeomorphic.
On the other hand, there is no homeomorphism from the torus to, for instance, the sphere, signifying that these represent two topologically distinct spaces. Part of topology is concerned with studying homeomorphism-invariants of topological spaces (“topological properties”) which allow to detect by means of algebraic manipulations whether two topological spaces are homeomorphic (or more generally homotopy equivalent) or not. This is called algebraic topology. A basic algebraic invariant is the fundamental group of a topological space (discussed below), which measures how many ways there are to wind loops inside a topological space.
Beware the popular imagery of “rubber-sheet geometry”, which only captures part of the full scope of topology, in that it invokes spaces that locally still look like metric spaces (called topological manifolds, see below). But the concept of topological spaces is a good bit more general. Notably, finite topological spaces are either discrete or very much unlike metric spaces (example below); the former play a role in categorical logic. Also, in geometry, exotic topological spaces frequently arise when forming non-free quotients. In order to gauge just how many of such “exotic” examples of topological spaces beyond locally metric spaces one wishes to admit in the theory, extra “separation axioms” are imposed on topological spaces (see below), and the flavour of topology as a field depends on this choice.
Among the separation axioms, the Hausdorff space axiom is the most popular (see below). But the weaker axiom of sobriety (see below) stands out, because on the one hand it is the weakest axiom that is still naturally satisfied in applications to algebraic geometry (schemes are sober) and computer science (Vickers 89), and on the other, it fully realizes the strong roots that topology has in formal logic: sober topological spaces are entirely characterized by the union-, intersection- and inclusion-relations (logical conjunction, disjunction and implication) among their open subsets (propositions). This leads to a natural and fruitful generalization of topology to more general “purely logic-determined spaces”, called locales, and in yet more generality, toposes and higher toposes. While the latter are beyond the scope of this introduction, their rich theory and relation to the foundations of mathematics and geometry provide an outlook on the relevance of the basic ideas of topology.
In this first part we discuss the foundations of the concept of “sets equipped with topology” (topological spaces) and of continuous functions between them.
The proofs in the following freely use the principle of excluded middle, hence proof by contradiction, and in a few places they also use the axiom of choice/Zorn's lemma.
Hence we discuss topology in its traditional form with classical logic.
We do however highlight the role of frame homomorphisms (def. below) and that of sober topological spaces (def. below). These concepts pave the way to a constructive formulation of topology in terms not of topological spaces but in terms of locales (remark below). For further reading along these lines see Johnstone 83.
Apart from classical logic, we assume the usual informal concept of sets. The reader (only) needs to know the concepts of
-
complements of subsets;
-
image sets and pre-image sets under a function
;
-
unions and intersections of indexed sets of subsets .
The only rules of set theory that we use are the
For reference, we recall these:
Proposition
(images preserve unions but not in general intersections)
Let be a function between sets. Let be a set of subsets of . Then
-
(the image under of a union of subsets is the union of the images)
-
(the image under of the intersection of the subsets is contained in the intersection of the images).
The injection in the second item is in general proper. If is an injective function and if is non-empty, then this is a bijection:
Proposition
(pre-images preserve unions and intersections)
Let be a function between sets. Let be a set of subsets of . Then
-
(the pre-image under of a union of subsets is the union of the pre-images),
-
(the pre-image under of the intersection of the subsets is the intersection of the pre-images).
Proposition
Given a set and a set of subsets
then the complement of their union is the intersection of their complements
and the complement of their intersection is the union of their complements
Moreover, taking complements reverses inclusion relations:
Metric spaces
The concept of continuity was first made precise in analysis, in terms of epsilontic analysis on metric spaces, recalled as def. below. Then it was realized that this has a more elegant formulation in terms of the more general concept of open sets, this is prop. below. Adopting the latter as the definition leads to a more abstract concept of “continuous space”, this is the concept of topological spaces, def. below.
Here we briefly recall the relevant basic concepts from analysis, as a motivation for various definitions in topology. The reader who either already recalls these concepts in analysis or is content with ignoring the motivation coming from analysis should skip right away to the section Topological spaces.
Definition
A metric space is
-
a set (the “underlying set”);
-
a function (the “distance function”) from the Cartesian product of the set with itself to the non-negative real numbers
such that for all :
-
(symmetry)
-
(non-degeneracy)
Definition
Let , be a metric space. Then for every element and every a positive real number, we write
for the open ball of radius around . Similarly we write
for the closed ball of radius around . Finally we write
for the sphere of radius around .
For we also speak of the unit open/closed ball and the unit sphere.
Definition
For a metric space (def. ) then a subset is called a bounded subset if is contained in some open ball (def. )
around some of some radius .
A key source of metric spaces are normed vector spaces:
Definition
(normed vector space)
A normed vector space is
-
from the underlying set of to the non-negative real numbers,
such that for all with absolute value and all it holds true that
-
(linearity) ;
-
(non-degeneracy) if then .
Proposition
Every normed vector space becomes a metric space according to def. by setting
Examples of normed vector spaces (def. ) and hence, via prop. , of metric spaces include the following:
Example
For , the Cartesian space
carries a norm (the Euclidean norm ) given by the square root of the sum of the squares of the components:
Via prop. this gives the structure of a metric space, and as such it is called the Euclidean space of dimension .
Example

More generally, for , and , , then the Cartesian space carries the p-norm
One also sets
and calls this the supremum norm.
The graphics on the right (grabbed from Wikipedia) shows unit circles (def. ) in with respect to various p-norms.
By the Minkowski inequality, the p-norm generalizes to non-finite dimensional vector spaces such as sequence spaces and Lebesgue spaces.
Continuity
The following is now the fairly obvious definition of continuity for functions between metric spaces.
Definition
(epsilontic definition of continuity)
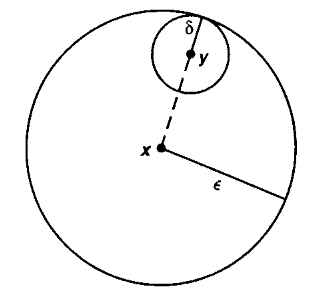
For and two metric spaces (def. ), then a function
is said to be continuous at a point if for every positive real number there exists a positive real number such that for all that are a distance smaller than from then their image is a distance smaller than from :
The function is said to be continuous if it is continuous at every point .
Example
(distance function from a subset is continuous)
Let be a metric space (def. ) and let be a subset of the underlying set. Define then the function
from the underlying set to the real numbers by assigning to a point the infimum of the distances from to , as ranges over the elements of :
This is a continuous function, with regarded as a metric space via its Euclidean norm (example ).
In particular the original distance function is continuous in both its arguments.
Proof
Let and let be a positive real number. We need to find a positive real number such that for with then .
For and , consider the triangle inequalities
Forming the infimum over of all terms appearing here yields
which implies
This means that we may take for instance .
Example
(rational functions are continuous)
Consider the real line regarded as the 1-dimensional Euclidean space from example .
For a polynomial, then the function
is a continuous function in the sense of def. . Hence polynomials are continuous functions.
Similarly rational functions are continuous on their domain of definition: for two polynomials, then is a continuous function.
Also for instance forming the square root is a continuous function .
On the other hand, a step function is continuous everywhere except at the finite number of points at which it changes its value, see example below.
We now reformulate the analytic concept of continuity from def. in terms of the simple but important concept of open sets:
Definition
(neighbourhood and open set)
Let be a metric space (def. ). Say that:
-
A neighbourhood of a point is a subset which contains some open ball around (def. ).
-
An open subset of is a subset such that for every it also contains an open ball around (def. ).
-
An open neighbourhood of a point is a neighbourhood of which is also an open subset, hence equivalently this is any open subset of that contains .
The following picture shows a point , some open balls containing it, and two of its neighbourhoods :
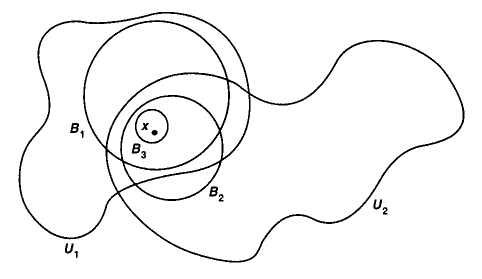
graphics grabbed from Munkres 75
Example
(the empty subset is open)
Notice that for a metric space, then the empty subset is always an open subset of according to def. . This is because the clause for open subsets says that “for every point there exists…”, but since there is no in , this clause is always satisfied in this case.
Conversely, the entire set is always an open subset of .
Example
(open/closed intervals)
Regard the real numbers as the 1-dimensional Euclidean space (example ).
For consider the following subsets:
-
(open interval)
-
(half-open interval)
-
(half-open interval)
-
(closed interval)
The first of these is an open subset according to def. , the other three are not. The first one is called an open interval, the last one a closed interval and the middle two are called half-open intervals.
Similarly for one considers
-
(unbounded open interval)
-
(unbounded open interval)
-
(unbounded half-open interval)
-
(unbounded half-open interval)
The first two of these are open subsets, the last two are not.
For completeness we may also consider
We may now rephrase the analytic definition of continuity entirely in terms of open subsets (def. ):
Proposition
(rephrasing continuity in terms of open sets)
Let and be two metric spaces (def. ). Then a function is continuous in the epsilontic sense of def. precisely if it has the property that its pre-images of open subsets of (in the sense of def. ) are open subsets of :
principle of continuity
Continuous pre-Images of open subsets are open.
Proof
Observe, by direct unwinding the definitions, that the epsilontic definition of continuity (def. ) says equivalently in terms of open balls (def. ) that is continuous at precisely if for every open ball around an image point, there exists an open ball around the corresponding pre-image point which maps into it:
With this observation the proof immediate. For the record, we spell it out:
First assume that is continuous in the epsilontic sense. Then for any open subset and any point in the pre-image, we need to show that there exists an open neighbourhood of in .
That is open in means by definition that there exists an open ball in around for some radius . By the assumption that is continuous and using the above observation, this implies that there exists an open ball in such that , hence such that . Hence this is an open ball of the required kind.
Conversely, assume that the pre-image function takes open subsets to open subsets. Then for every and an open ball around its image, we need to produce an open ball around such that .
But by definition of open subsets, is open, and therefore by assumption on its pre-image is also an open subset of . Again by definition of open subsets, this implies that it contains an open ball as required.
Example
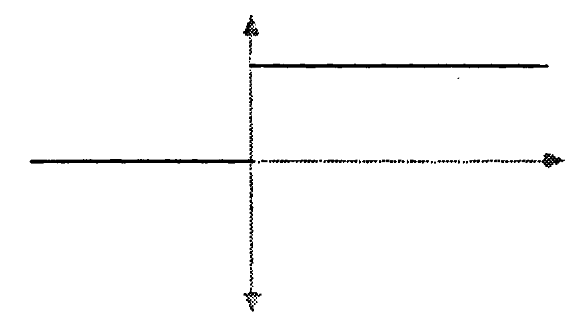
Consider as the 1-dimensional Euclidean space (example ) and consider the step function
graphics grabbed from Vickers 89
Consider then for the open interval , an open subset according to example . The preimage of this open subset is
By example , all except the last of these pre-images listed are open subsets.
The failure of the last of the pre-images to be open witnesses that the step function is not continuous at .
Compactness
A key application of metric spaces in analysis is that they allow a formalization of what it means for an infinite sequence of elements in the metric space (def. below) to converge to a limit of a sequence (def. below). Of particular interest are therefore those metric spaces for which each sequence has a converging subsequence: the sequentially compact metric spaces (def. ).
We now briefly recall these concepts from analysis. Then, in the above spirit, we reformulate their epsilontic definition in terms of open subsets. This gives a useful definition that generalizes to topological spaces, the compact topological spaces discussed further below.
Definition
(sequence)
Given a set , then a sequence of elements in is a function
from the natural numbers to .
A sub-sequence of such a sequence is a sequence of the form
Definition
(convergence to limit of a sequence)
Let be a metric space (def. ). Then a sequence
in the underlying set (def. ) is said to converge to a point , denoted
if for every positive real number , there exists a natural number , such that all elements in the sequence after the th one have distance less than from .
Here the point is called the limit of the sequence. Often one writes for this point.
Definition
Given a metric space (def. ), then a sequence of points in (def. )
is called a Cauchy sequence if for every positive real number there exists a natural number such that the distance between any two elements of the sequence beyond the th one is less than
Definition
A metric space (def. ), for which every Cauchy sequence (def. ) converges (def. ) is called a complete metric space.
A normed vector space, regarded as a metric space via prop. that is complete in this sense is called a Banach space.
Finally recall the concept of compactness of metric spaces via epsilontic analysis:
Definition
(sequentially compact metric space)
A metric space (def. ) is called sequentially compact if every sequence in has a subsequence (def. ) which converges (def. ).
The key fact to translate this epsilontic definition of compactness to a concept that makes sense for general topological spaces (below) is the following:
Proposition
(sequentially compact metric spaces are equivalently compact metric spaces)
For a metric space (def. ) the following are equivalent:
-
for every set of open subsets of (def. ) which cover in that , then there exists a finite subset of these open subsets which still covers in that also .
The proof of prop. is most conveniently formulated with some of the terminology of topology in hand, which we introduce now. Therefore we postpone the proof to below.
In summary prop. and prop. show that the purely combinatorial and in particular non-epsilontic concept of open subsets captures a substantial part of the nature of metric spaces in analysis. This motivates to reverse the logic and consider more general “spaces” which are only characterized by what counts as their open subsets. These are the topological spaces which we turn to now in def. (or, more generally, these are the “locales”, which we briefly consider below in remark ).
Topological spaces
Due to prop. we should pay attention to open subsets in metric spaces. It turns out that the following closure property, which follow directly from the definitions, is at the heart of the concept:
Proposition
(closure properties of open sets in a metric space)
The collection of open subsets of a metric space as in def. has the following properties:
-
The union of any set of open subsets is again an open subset.
-
The intersection of any finite number of open subsets is again an open subset.
Remark
(empty union and empty intersection)
Notice the degenerate case of unions and intersections of subsets for the case that they are indexed by the empty set :
-
the empty union is the empty set itself;
-
the empty intersection is all of .
(The second of these may seem less obvious than the first. We discuss the general logic behind these kinds of phenomena below.)
This way prop. is indeed compatible with the degenerate cases of examples of open subsets in example .
Proposition motivates the following generalized definition, which abstracts away from the concept of metric space just its system of open subsets:
Definition
Given a set , then a topology on is a collection of subsets of called the open subsets, hence a subset of the power set
such that this is closed under forming
-
finite intersections;
-
arbitrary unions.
- the empty set is in (being the union of no subsets)
and
- the whole set itself is in (being the intersection of no subsets).
A set equipped with such a topology is called a topological space.
Remark
In the field of topology it is common to eventually simply say “space” as shorthand for “topological space”. This is especially so as further qualifiers are added, such as “Hausdorff space” (def. below). But beware that there are other kinds of spaces in mathematics.
In view of example below one generalizes the terminology from def. as follows:
Definition
Let be a topological space and let be a point. A neighbourhood of is a subset which contains an open subset that still contains .
An open neighbourhood is a neighbourhood that is itself an open subset, hence an open neighbourhood of is the same as an open subset containing .
Remark
The simple definition of open subsets in def. and the simple implementation of the principle of continuity below in def. gives the field of topology its fundamental and universal flavor. The combinatorial nature of these definitions makes topology be closely related to formal logic. This becomes more manifest still for the “sober topological space” discussed below. For more on this perspective see the remark on locales below, remark . An introductory textbook amplifying this perspective is (Vickers 89).
Before we look at first examples below, here is some common further terminology regarding topological spaces:
There is an evident partial ordering on the set of topologies that a given set may carry:
Definition
Let be a set, and let be two topologies on , hence two choices of open subsets for , making it a topological space. If
hence if every open subset of with respect to is also regarded as open by , then one says that
With any kind of structure on sets, it is of interest how to “generate” such structures from a small amount of data:
Definition
Let be a topological space, def. , and let
be a subset of its set of open subsets. We say that
-
is a basis for the topology if every open subset is a union of elements of ;
-
is a sub-basis for the topology if every open subset is a union of finite intersections of elements of .
Often it is convenient to define topologies by defining some (sub-)basis as in def. . Examples are the the metric topology below, example , the binary product topology in def. below, and the compact-open topology on mapping spaces below in def. . To make use of this, we need to recognize sets of open subsets that serve as the basis for some topology:
Lemma
(recognition of topological bases)
Let be a set.
-
A collection of subsets of is a basis for some topology (def. ) precisely if
-
every point of is contained in at least one element of ;
-
for every two subsets and for every point in their intersection, there exists a that contains and is contained in the intersection: .
-
-
A subset of open subsets is a sub-basis for a topology on precisely if is the coarsest topology (def. ) which contains .
Examples
We discuss here some basic examples of topological spaces (def. ), to get a feeling for the scope of the concept. But topological spaces are ubiquituous in mathematics, so that there are many more examples and many more classes of examples than could be listed. As we further develop the theory below, we encounter more examples, and more classes of examples. Below in Universal constructions we discuss a very general construction principle of new topological space from given ones.
First of all, our motivating example from above now reads as follows:
Example
Let be a metric space (def. ). Then the collection of its open subsets in def. constitutes a topology on the set , making it a topological space in the sense of def. . This is called the metric topology.
The open balls in a metric space constitute a basis of a topology (def. ) for the metric topology.
While the example of metric space topologies (example ) is the motivating example for the concept of topological spaces, it is important to notice that the concept of topological spaces is considerably more general, as some of the following examples show.
The following simplistic example of a (metric) topological space is important for the theory (for instance in prop. ):
Example
(empty space and point space)
On the empty set there exists a unique topology making it a topological space according to def. . We write also
for the resulting topological space, which we call the empty topological space.
On a singleton set there exists a unique topology making it a topological space according to def. , namelyf
We write
for this topological space and call it the point topological space.
This is equivalently the metric topology (example ) on , regarded as the 0-dimensional Euclidean space (example ).
Example
On the 2-element set there are (up to permutation of elements) three distinct topologies:
-
the codiscrete topology (def. ) ;
-
the discrete topology (def. ), ;
-
the Sierpinski space topology .
Example
The following shows all the topologies on the 3-element set (up to permutation of elements)
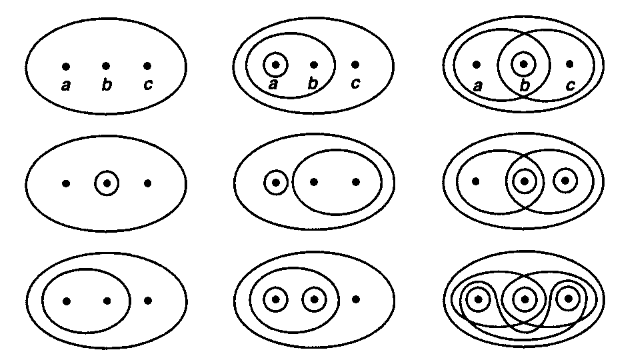
graphics grabbed from Munkres 75
Example
(discrete and co-discrete topology)
Let be any set. Then there are always the following two extreme possibilities of equipping with a topology in the sense of def. , and hence making it a topological space:
-
the set of all open subsets;
this is called the discrete topology on , it is the finest topology (def. ) on ,
we write for the resulting topological space;
-
the set containing only the empty subset of and all of itself;
this is called the codiscrete topology on , it is the coarsest topology (def. ) on ,
we write for the resulting topological space.
The reason for this terminology is best seen when considering continuous functions into or out of these (co-)discrete topological spaces, we come to this in example below.
Example
Given a set , then the cofinite topology or finite complement topology on is the topology (def. ) whose open subsets are precisely
-
all cofinite subsets (i.e. those such that the complement is a finite set);
-
the empty set.
If is itself a finite set (but not otherwise) then the cofinite topology on coincides with the discrete topology on (example ).
We now consider basic construction principles of new topological spaces from given ones:
-
disjoint union spaces (example )
-
subspaces (example ),
-
quotient spaces (example )
-
product spaces (example ).
Below in Universal constructions we will recognize these as simple special cases of a general construction principle.
Example
For a set of topological spaces, then their disjoint union
is the topological space whose underlying set is the disjoint union of the underlying sets of the summand spaces, and whose open subsets are precisely the disjoint unions of the open subsets of the summand spaces.
In particular, for any index set, then the disjoint union of copies of the point space (example ) is equivalently the discrete topological space (example ) on that index set:
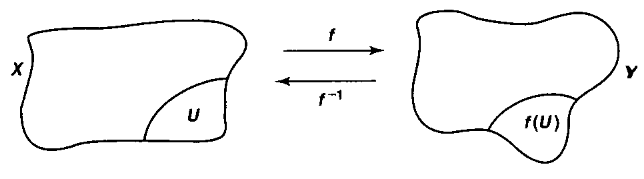
Example
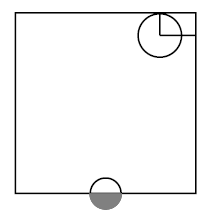
Let be a topological space, and let be a subset of the underlying set. Then the corresponding topological subspace has as its underlying set, and its open subsets are those subsets of which arise as restrictions of open subsets of .
(This is also called the initial topology of the inclusion map. We come back to this below in def. .)
The picture on the right shows two open subsets inside the square, regarded as a topological subspace of the plane :
graphics grabbed from Munkres 75
Example
Let be a topological space (def. ) and let
be an equivalence relation on its underlying set. Then the quotient topological space has
- as underlying set the quotient set , hence the set of equivalence classes,
and
-
a subset is declared to be an open subset precisely if its preimage under the canonical projection map
is open in .
(This is also called the final topology of the projection . We come back to this below in def. . )
Often one considers this with input datum not the equivalence relation, but any surjection
of sets. Of course this identifies with . Hence the quotient topology on the codomain set of a function out of any topological space has as open subsets those whose pre-images are open.
To see that this indeed does define a topology on it is sufficient to observe that taking pre-images commutes with taking unions and with taking intersections.
Example
(binary product topological space)
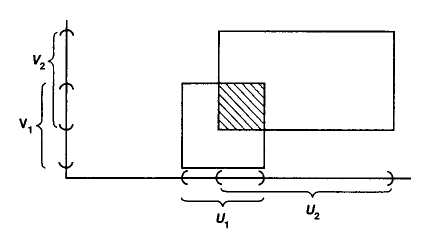
For and two topological spaces, then their binary product topological space has as underlying set the Cartesian product of the corresponding two underlying sets, and its topology is generated from the basis (def. ) given by the Cartesian products of the opens .
graphics grabbed from Munkres 75
Beware for non-finite products, the descriptions of the product topology is not as simple. This we turn to below in example , after introducing the general concept of limits in the category of topological spaces.
The following examples illustrate how all these ingredients and construction principles may be combined.
The following example examines in more detail below in example , after we have introduced the concept of homeomorphisms below.
Example
Consider the real numbers as the 1-dimensional Euclidean space (example ) and hence as a topological space via the corresponding metric topology (example ). Moreover, consider the closed interval from example , regarded as a subspace (def. ) of .
The product space (example ) of this interval with itself
is a topological space modelling the closed square. The quotient space (example ) of that by the relation which identifies a pair of opposite sides is a model for the cylinder. The further quotient by the relation that identifies the remaining pair of sides yields a model for the torus.
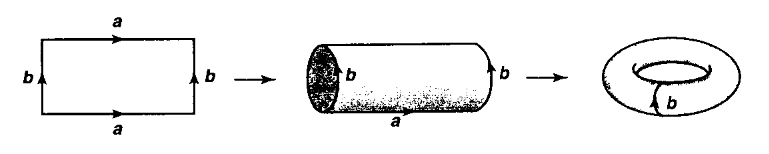
graphics grabbed from Munkres 75
Example
(spheres and disks)
For write
-
for the n-disk, the closed unit ball (def. ) in the -dimensional Euclidean space (example ) and equipped with the induced subspace topology (example ) of the corresponding metric topology (example );
-
for the (n-1)-sphere (def. ) also equipped with the corresponding subspace topology;
-
for the continuous function that exhibits this boundary inclusion.
Notice that
-
is the empty topological space (example );
-
is the disjoint union space (example ) of the point topological space (example ) with itself, equivalently the discrete topological space on two elements (example ).
The following important class of topological spaces form the foundation of algebraic geometry:
Example
(Zariski topology on affine space)
Let be a field, let , and write for the set of polynomials in variables over .
For a subset of polynomials, let the subset of the -fold Cartesian product of the underlying set of (the vanishing set of ) be the subset of points on which all these polynomials jointly vanish:
These subsets are called the Zariski closed subsets.
Write
for the set of complements of the Zariski closed subsets. These are called the Zariski open subsets of .
The Zariski open subsets of form a topology (def. ), called the Zariski topology. The resulting topological space
is also called the -dimensional affine space over .
More generally:
Example
(Zariski topology on the prime spectrum of a commutative ring)
Let be a commutative ring. Write for its set of prime ideals. For any subset of elements of the ring, consider the subsets of those prime ideals that contain :
These are called the Zariski closed subsets of . Their complements are called the Zariski open subsets.
Then the collection of Zariski open subsets in its set of prime ideals
satisfies the axioms of a topology (def. ), the Zariski topology.
This topological space
is called (the space underlying) the prime spectrum of the commutative ring.
Closed subsets
The complements of open subsets in a topological space are called closed subsets (def. below). This simple definition indeed captures the concept of closure in the analytic sense of convergence of sequences (prop. below). Of particular interest for the theory of topological spaces in the discussion of separation axioms below are those closed subsets which are “irreducible” (def. below). These happen to be equivalently the “frame homomorphisms” (def. ) to the frame of opens of the point (prop. below).
Definition
Let be a topological space (def. ).
-
A subset is called a closed subset if its complement is an open subset:
graphics grabbed from Vickers 89
-
If a singleton subset is closed, one says that is a closed point of .
-
Given any subset , then its topological closure is the smallest closed subset containing :
-
A subset such that is called a dense subset of .
Often it is useful to reformulate def. of closed subsets as follows:
Lemma
(alternative characterization of topological closure)
Let be a topological space and let be a subset of its underlying set. Then a point is contained in the topological closure (def. ) precisely if every open neighbourhood of (def. ) intersects :
Proof
Due to de Morgan duality (prop. ) we may rephrase the definition of the topological closure as follows:
Proposition
(closure of a finite union is the union of the closures)
For a finite set and a finite set of subsets of a topological space, we have
Proof
By lemma we use that a point is in the closure of a set precisely if every open neighbourhood (def. ) of the point intersects the set.
Hence in one direction
because if every neighbourhood of a point intersects some , then every neighbourhood intersects their union.
The other direction
is equivalent by de Morgan duality to
On left now we have the point for which there exists for each a neighbourhood which does not intersect . Since is finite, the intersection is still an open neighbourhood of , and such that it intersects none of the , hence such that it does not intersect their union. This implis that the given point is contained in the set on the right.
Definition
(topological interior and boundary)
Let be a topological space (def. ) and let be a subset. Then the topological interior of is the largest open subset still contained in , :
The boundary of is the complement of its interior inside its topological closure (def. ):
Lemma
(duality between closure and interior)
Let be a topological space and let be a subset. Then the topological interior of (def. ) is the same as the complement of the topological closure of the complement of :
and conversely
Example
(topological closure and interior of closed and open intervals)
Regard the real numbers as the 1-dimensional Euclidean space (example ) and equipped with the corresponding metric topology (example ) . Let . Then the topological interior (def. ) of the closed interval (example ) is the open interval , moreover the closed interval is its own topological closure (def. ) and the converse holds (by lemma ):
Hence the boundary of the closed interval is its endpoints, while the boundary of the open interval is empty
The terminology “closed” subspace for complements of opens is justified by the following statement, which is a further example of how the combinatorial concept of open subsets captures key phenomena in analysis:
Proposition
(convergence in closed subspaces)
Let be a metric space (def. ), regarded as a topological space via example , and let be a subset. Then the following are equivalent:
-
is a closed subspace according to def. .
-
For every sequence (def. ) with elements in , which converges as a sequence in (def. ) to some , we have .
Proof
First assume that is closed and that for some . We need to show that then . Suppose it were not, hence that . Since, by assumption on , this complement is an open subset, it would follow that there exists a real number such that the open ball around of radius were still contained in the complement: . But since the sequence is assumed to converge in , this would mean that there exists such that all are in , hence in . This contradicts the assumption that all are in , and hence we have proved by contradiction that .
Conversely, assume that for all sequences in that converge to some then . We need to show that then is closed, hence that is an open subset, hence that for every we may find a real number such that the open ball around of radius is still contained in . Suppose on the contrary that such did not exist. This would mean that for each with then the intersection were non-empty. Hence then we could choose points in these intersections. These would form a sequence which clearly converges to the original , and so by assumption we would conclude that , which violates the assumption that . Hence we proved by contradiction is in fact open.
Often one considers closed subsets inside a closed subspace. The following is immediate, but useful.
Lemma
(subsets are closed in a closed subspace precisely if they are closed in the ambient space)
Let be a topological space (def. ), and let be a closed subset (def. ), regarded as a topological subspace (example ). Then a subset is a closed subset of precisely if it is closed as a subset of .
Proof
If is closed in this means equivalently that there is an open subset in such that
But by the definition of the subspace topology, this means equivalently that there is a subset which is open in such that . Hence the above is equivalent to the existence of an open subset such that
But now the condition that itself is a closed subset of means equivalently that there is an open subset with . Hence the above is equivalent to the existence of two open subsets such that
Since the union is again open, this implies that is closed in .
Conversely, that is closed in means that there exists an open with . This means that , and since is open in by definition of the subspace topology, this means that is closed in .
A special role in the theory is played by the “irreducible” closed subspaces:
Definition
A closed subset (def. ) of a topological space is called irreducible if it is non-empty and not the union of two closed proper (i.e. smaller) subsets. In other words, a non-empty closed subset is irreducible if whenever are two closed subspace such that
then or .
Example
(closures of points are irreducible)
For a point inside a topological space, then the closure of the singleton subset is irreducible (def. ).
Example
(no nontrivial closed irreducibles in metric spaces)
Let be a metric space, regarded as a topological space via its metric topology (example ). Then every point is closed (def ), hence every singleton subset is irreducible according to def. .
Let be the 1-dimensional Euclidean space (example ) with its metric topology (example ). Then for the closed interval (example ) is not irreducible, since for any with it is the union of two smaller closed subintervals:
In fact we will see below (prop. ) that in a metric space the singleton subsets are precisely the only irreducible closed subsets.
Often it is useful to re-express the condition of irreducibility of closed subspaces in terms of complementary open subsets:
Proposition
(irreducible closed subsets in terms of prime open subsets)
Let be a topological space, and let be a proper open subset of , hence so that the complement is a non-empty closed subspace. Then is irreducible in the sense of def. precisely if whenever are open subsets with then or :
The open subsets with this property are also called the prime open subsets in .
Proof
Observe that every closed subset may be exhibited as the complement
of some open subset with respect to . Observe that under this identification the condition that is equivalent to the condition that , because it is equivalent to the equation labeled in the following sequence of equations:
Similarly, the condition that is equivalent to the condition that , because it is equivalent to the equality in the following sequence of equalities:
Under these identifications, the two conditions are manifestly the same.
We consider yet another equivalent characterization of irreducible closed subsets, prop. below, which will be needed in the discussion of the separation axioms further below. Stating this requires the following concept of “frame” homomorphism, the natural kind of homomorphisms between topological spaces if we were to forget the underlying set of points of a topological space, and only remember the set with its operations induced by taking finite intersections and arbitrary unions:
Definition
(frame homomorphisms)
Let and be topological spaces (def. ). Then a function
between their sets of open subsets is called a frame homomorphism from to if it preserves
-
arbitrary unions;
In other words, is a frame homomorphism precisely if
-
for every set and every -indexed set of elements of , then
-
for every finite set and every -indexed set of elements in , then
Remark
(frame homomorphisms preserve inclusions)
A frame homomorphism as in def. necessarily also preserves inclusions in that
-
for every inclusion with then
This is because inclusions are witnessed by unions
or alternatively because inclusions are witnessed by finite intersections:
Example
(pre-images of continuous functions are frame homomorphisms)
Let and be two topological spaces. One way to obtain a function between their sets of open subsets
is to specify a function
of their underlying sets, and take to be the pre-image operation. A priori this is a function of the form
and hence in order for this to co-restrict to when restricted to we need to demand that, under , pre-images of open subsets of are open subsets of . Below in def. we highlight these as the continuous functions between topological spaces.
In this case then
is a frame homomorphism from to in the sense of def. , by prop. .
For the following recall from example the point topological space .
Proposition
(irreducible closed subsets are equivalently frame homomorphisms to opens of the point)
For a topological space, then there is a natural bijection between the irreducible closed subspaces of (def. ) and the frame homomorphisms from to , and this bijection is given by
where is the union of all elements such that :
See also (Johnstone 82, II 1.3).
Proof
First we need to show that the function is well defined in that given a frame homomorphism then is indeed an irreducible closed subspace.
To that end observe that:
If there are two elements with then or .
This is because
where the first equality holds because preserves finite intersections by def. , the inclusion holds because respects inclusions by remark , and the second equality holds because preserves arbitrary unions by def. . But in the intersection of two open subsets is empty precisely if at least one of them is empty, hence or . But this means that or , as claimed.
Now according to prop. the condition identifies the complement as an irreducible closed subspace of .
Conversely, given an irreducible closed subset , define by
This does preserve
-
arbitrary unions
because precisely if which is the case precisely if all , which means that all and because ;
while as soon as one of the is not contained in , which means that one of the which means that ;
-
finite intersections
because if , then by or , whence or , whence with also ;
while if is not contained in then neither nor is contained in and hence with also .
Hence this is indeed a frame homomorphism .
Finally, it is clear that these two operations are inverse to each other.
Continuous functions
With the concept of topological spaces in hand (def. ) it is now immediate to formally implement in abstract generality the statement of prop. :
principle of continuity
Continuous pre-Images of open subsets are open.
Definition
(continuous function)
A continuous function between topological spaces (def. )
is a function between the underlying sets,
such that pre-images under of open subsets of are open subsets of .
We may equivalently state this in terms of closed subsets:
Proposition
Let and be two topological spaces (def. ). Then a function
between the underlying sets is continuous in the sense of def. precisely if pre-images under of closed subsets of (def. ) are closed subsets of .
Proof
This follows since taking pre-images commutes with taking complements.
Before looking at first examples of continuous functions below we consider now an informal remark on the resulting global structure, the “category of topological spaces”, remark below. This is a language that serves to make transparent key phenomena in topology which we encounter further below, such as the Tn-reflection (remark below), and the universal constructions.
Remark
(concrete category of topological spaces)
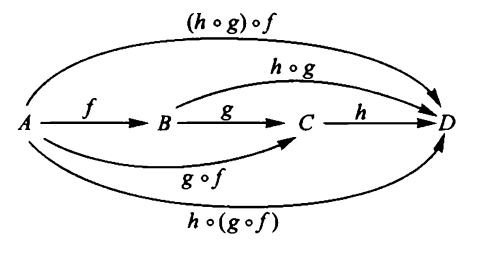
For three topological spaces and for
two continuous functions (def. ) then their composition
is clearly itself again a continuous function from to .
Moreover, this composition operation is clearly associative, in that for
three continuous functions, then
Finally, the composition operation is also clearly unital, in that for each topological space there exists the identity function and for any continuous function then
One summarizes this situation by saying that:
-
topological spaces constitute the objects,
-
continuous functions constitute the morphisms (homomorphisms)
of a category, called the category of topological spaces (“Top” for short).
It is useful to depict collections of objects with morphisms between them by diagrams, like this one:
graphics grabbed from Lawvere-Schanuel 09.
There are other categories. For instance there is the category of sets (“Set” for short) whose
The two categories Top and Set are different, but related. After all,
-
an object of Top (hence a topological space) is an object of Set (hence a set) equipped with extra structure (namely with a topology);
-
a morphism in Top (hence a continuous function) is a morphism in Set (hence a plain function) with the extra property that it preserves this extra structure.
Hence we have the underlying set assigning function
from the class of topological spaces to the class of sets. But more is true: every continuous function between topological spaces is, by definition, in particular a function on underlying sets:
and this assignment (trivially) respects the composition of morphisms and the identity morphisms.
Such a function between classes of objects of categories, which is extended to a function on the sets of homomorphisms between these objects in a way that respects composition and identity morphisms is called a functor. If we write an arrow between categories
then it is understood that we mean not just a function between their classes of objects, but a functor.
The functor at hand has the special property that it does not do much except forgetting extra structure, namely the extra structure on a set given by a choice of topology . One also speaks of a forgetful functor.
This is intuitively clear, and we may easily formalize it: The functor has the special property that as a function between sets of homomorphisms (“hom sets”, for short) it is injective. More in detail, given topological spaces and then the component function of from the set of continuous function between these spaces to the set of plain functions between their underlying sets
is an injective function, including the continuous functions among all functions of underlying sets.
A functor with this property, that its component functions between all hom-sets are injective, is called a faithful functor.
A category equipped with a faithful functor to Set is called a concrete category.
Hence Top is canonically a concrete category.
Example
(product topological space construction is functorial)
For and two categories as in remark (for instance Top or Set) then we obtain a new category denoted and called their product category whose
-
morphisms are pairs with a morphism of
and a morphism of ,
-
composition of morphisms is defined pairwise .
This concept secretly underlies the construction of product topological spaces:
Let , , and be topological spaces. Then for all pairs of continuous functions
and
the canonically induced function on Cartesian products of sets
is clearly a continuous function with respect to the binary product space topologies (def. )
Moreover, this construction respects identity functions and composition of functions in both arguments.
In the language of category theory (remark ), this is summarized by saying that the product topological space construction extends to a functor from the product category of the category Top with itself to itself:
Examples
We discuss here some basic examples of continuous functions (def. ) between topological spaces (def. ) to get a feeling for the nature of the concept. But as with topological spaces themselves, continuous functions between them are ubiquitous in mathematics, and no list will exhaust all classes of examples. Below in the section Universal constructions we discuss a general principle that serves to produce examples of continuous functions with prescribed “universal properties”.
Example
(point space is terminal)
For any topological space, then there is a unique continuous function
-
from the empty topological space (def. )
-
from to the point topological space (def. ).
In the language of category theory (remark ), this says that
-
the empty topological space is the initial object
-
the point space is the terminal object
in the category Top of topological spaces. We come back to this below in example .
Example
(constant continuous functions)
For a topological space then for any element of the underlying set, there is a unique continuous function (which we denote by the same symbol)
from the point topological space (def. ), whose image in is that element. Hence there is a natural bijection
between the continuous functions from the point to any topological space, and the underlying set of that topological space.
More generally, for and two topological spaces, then a continuous function between them is called a constant function with value some point if it factors through the point spaces as
Definition
For , two topological spaces, then a continuous function (def. ) is called locally constant if every point has a neighbourhood (def. ) on which the function is constant.
Example
(continuous functions into and out of discrete and codiscrete spaces)
Let be a set and let be a topological space. Recall from example
on the underlying set . Then continuous functions (def. ) into/out of these satisfy:
-
every function (of sets) out of a discrete space is continuous;
-
every function (of sets) into a codiscrete space is continuous.
Also:
- every continuous function into a discrete space is locally constant (def. ).
Example
(diagonal)
For a set, its diagonal is the function from to the Cartesian product of with itself, given by
For a topological space, then the diagonal is a continuous function to the product topological space (def. ) of with itself.
To see this, it is sufficient to see that the preimages of basic opens in are in . But these pre-images are the intersections , which are open by the axioms on the topology .
Example
Let be a continuous function.
Write for the image of on underlying sets, and consider the resulting factorization of through on underlying sets:
There are the following two ways to topologize the image such as to make this a sequence of two continuous functions:
-
By example inherits a subspace topology from which evidently makes the inclusion a continuous function.
Observe that this also makes a continuous function: An open subset of in this case is of the form for , and , which is open in since is continuous.
-
By example inherits a quotient topology from which evidently makes the surjection a continuous function.
Observe that this also makes a continuous function: The preimage under this map of an open subset is the restriction , and the pre-image of that under is , as before, which is open since is continuous, and therefore is open in the quotient topology.
Beware, in general a continuous function itself (as opposed to its pre-image function) neither preserves open subsets, nor closed subsets, as the following examples show:
Example
Regard the real numbers as the 1-dimensional Euclidean space (example ) equipped with the metric topology (example ). For the constant function (example )
maps every open subset to the singleton set , which is not open.
Example
Write for the set of real numbers equipped with its discrete topology (def. ) and for the set of real numbers equipped with its Euclidean metric topology (example , example ). Then the identity function on the underlying sets
is a continuous function (a special case of example ). A singleton subset is open, but regarded as a subset it is not open.
Example
Consider the set of real numbers equipped with its Euclidean metric topology (example , example ). The exponential function
maps all of (which is a closed subset, since ) to the open interval , which is not closed.
Those continuous functions that do happen to preserve open or closed subsets get a special name:
Definition
(open maps and closed maps)
A continuous function (def. ) is called
-
an open map if the image under of an open subset of is an open subset of ;
-
a closed map if the image under of a closed subset of (def. ) is a closed subset of .
Example
(image projections of open/closed maps are themselves open/closed)
If a continuous function is an open map or closed map (def. ) then so its its image projection , respectively, for regarded with its subspace topology (example ).
Proof
If is an open map, and is an open subset, so that is also open in , then, since , it is also still open in the subspace topology, hence is an open map.
If is a closed map, and is a closed subset so that also is a closed subset, then the complement is open in and hence is open in the subspace topology, which means that is closed in the subspace topology.
Example
(projections are open continuous functions )
For and two topological spaces, then the projection maps
out of their product topological space (def. )
are open continuous functions (def. ).
This is because, by definition, every open subset in the product space topology is a union of products of open subsets and in the factor spaces
and because taking the image of a function preserves unions of subsets
Below in prop. we find a large supply of closed maps.
Sometimes it is useful to recognize quotient topological space projections via saturated subsets (essentially another term for pre-images of underlying sets):
Definition
Let be a function of sets. Then a subset is called an -saturated subset (or just saturated subset, if is understood) if is the pre-image of its image:
Here is also called the -saturation of .
Example
(pre-images are saturated subsets)
For any function of sets, and any subset of , then the pre-image is an -saturated subset of (def. ).
Observe that:
Lemma
Let be a function. Then a subset is -saturated (def. ) precisely if its complement is saturated.
Proposition
(recognition of quotient topologies)
A continuous function (def. )
whose underlying function is surjective exhibits as the corresponding quotient topology (def. ) precisely if sends open and -saturated subsets in (def. ) to open subsets of . By lemma this is the case precisely if it sends closed and -saturated subsets to closed subsets.
We record the following technical lemma about saturated subspaces, which we will need below to prove prop. .
Lemma
(saturated open neighbourhoods of saturated closed subsets under closed maps)
Let
-
be a closed map (def. );
-
be a closed subset of (def. ) which is -saturated (def. );
-
be an open subset containing ;
then there exists a smaller open subset still containing
and such that is still -saturated.
Proof
We claim that the complement of by the -saturation (def. ) of the complement of by
has the desired properties. To see this, observe first that
-
the complement is closed, since is assumed to be open;
-
hence the image is closed, since is assumed to be a closed map;
-
hence the pre-image is closed, since is continuous (using prop. ), therefore its complement is indeed open;
-
this pre-image is saturated (by example ) and hence also its complement is saturated (by lemma ).
Therefore it now only remains to see that .
By de Morgan's law (prop. ) the inclusion is equivalent to the inclusion , which is clearly the case.
The inclusion is equivalent to . Since is saturated by assumption, this is equivalent to . This in turn holds precisely if . Since is saturated, this holds precisely if , and this is true by the assumption that .
Homeomorphisms
With the objects (topological spaces) and the morphisms (continuous functions) of the category Top thus defined (remark ), we obtain the concept of “sameness” in topology. To make this precise, one says that a morphism
in a category is an isomorphism if there exists a morphism going the other way around
which is an inverse in the sense that both its compositions with yield an identity morphism:
Since such is unique if it exists, one often writes “” for this inverse morphism.
Definition
An isomorphism in the category Top (remark ) of topological spaces (def. ) with continuous functions between them (def. ) is called a homeomorphism.
Hence a homeomorphism is a continuous function
between two topological spaces , such that there exists another continuous function the other way around
such that their composites are the identity functions on and , respectively:
graphics grabbed from Munkres 75
We notationally indicate that a continuous function is a homeomorphism by the symbol “”.
If there is some, possibly unspecified, homeomorphism between topological spaces and , then we also write
and say that the two topological spaces are homeomorphic.
A property/predicate of topological spaces which is invariant under homeomorphism in that
is called a topological property or topological invariant.
Remark
(notation for homeomorphisms)
Beware the following notation:
-
In topology the notation generally refers to the pre-image function of a given function , while if is a homeomorphism (def. ), it is also used for the inverse function of . This abuse of notation is convenient: If happens to be a homeomorphism, then the pre-image of a subsets under is its image under the inverse function .
-
Many authors strictly distinguish the symbols “” and “” and use the former to denote homeomorphisms and the latter to refer to homotopy equivalences (which we consider in part 2). We use either symbol (but mostly “”) for “isomorphism” in whatever the ambient category may be and try to make that context always unambiguously explicit.
Remark
If is a homeomorphism (def. ) with inverse continuous function , then
-
also is a homeomophism, with inverse continuous function ;
-
the underlying function of sets of a homeomorphism is necessarily a bijection, with inverse bijection .
But beware that not every continuous function which is bijective on underlying sets is a homeomorphism. While an inverse function will exists on the level of functions of sets, this inverse may fail to be continuous:
Counter Example
Consider the continuous function
from the half-open interval (def. ) to the unit circle (def. ), regarded as a topological subspace (example ) of the Euclidean plane (example ).
The underlying function of sets of is a bijection. The inverse function of sets however fails to be continuous at . Hence this is not a homeomorphism.
Indeed, below we see that the two topological spaces and are distinguished by topological invariants, meaning that they cannot be homeomorphic via any (other) choice of homeomorphism. For example is a compact topological space (def. ) while is not, and has a non-trivial fundamental group, while that of is trivial (this prop.).
Below in example we discuss a practical criterion under which continuous bijections are homeomorphisms after all. But immediate from the definitions is the following characterization:
Proposition
(homeomorphisms are the continuous and open bijections)
Let be a continuous function between topological spaces (def. ). Then the following are equivalence:
-
is a homeomorphism;
-
is a bijection and a closed map (def. ).
Proof
It is clear from the definition that a homeomorphism in particular has to be a bijection. The condition that the inverse function be continuous means that the pre-image function of sends open subsets to open subsets. But by being the inverse to , that pre-image function is equal to , regarded as a function on subsets:
Hence sends opens to opens precisely if does, which is the case precisely if is an open map, by definition. This shows the equivalence of the first two items. The equivalence between the first and the third follows similarly via prop. .
Now we consider some actual examples of homeomorphisms:
Example
(concrete point homeomorphic to abstract point space)
Let be a non-empty topological space, and let be any point. Regard the corresponding singleton subset as equipped with its subspace topology (example ). Then this is homeomorphic (def. ) to the abstract point space from example :
Example
(open interval homeomorphic to the real line)
Regard the real line as the 1-dimensional Euclidean space (example ) with its metric topology (example ).
Then the open interval (def. ) regarded with its subspace topology (example ) is homeomorphic (def.) to all of the real line
An inverse pair of continuous functions is for instance given (via example ) by
and
But there are many other choices for and that yield a homeomorphism.
Similarly, for all
-
the open intervals (example ) equipped with their subspace topology are all homeomorphic to each other,
-
the closed intervals are all homeomorphic to each other,
-
the half-open intervals of the form are all homeomorphic to each other;
-
the half-open intervals of the form are all homeomorphic to each other.
Generally, every open ball in (def. ) is homeomorphic to all of :
While mostly the interest in a given homeomorphism is in it being non-obvious from the definitions, many homeomorphisms that appear in practice exhibit “obvious re-identifications” for which it is of interest to leave them consistently implicit:
Example
(homeomorphisms between iterated product spaces)
Let , and be topological spaces.
Then:
-
There is an evident homeomorphism between the two ways of bracketing the three factors when forming their product topological space (def. ), called the associator:
-
There are evident homeomorphism between and its product topological space (def. ) with the point space (example ), called the left and right unitors:
and
-
There is an evident homeomorphism between the results of the two orders in which to form their product topological spaces (def. ), called the braiding:
Moreover, all these homeomorphisms are compatible with each other, in that they make the following diagrams commute (recall remark ):
-
(triangle identity)
-
(hexagon identities)
and
-
(symmetry)
In the language of category theory (remark ), all this is summarized by saying that the the functorial construction of product topological spaces (example ) gives the category Top of topological spaces the structure of a monoidal category which moreover is symmetrically braided.
From this, a basic result of category theory, the MacLane coherence theorem, guarantees that there is no essential ambiguity re-backeting arbitrary iterations of the binary product topological space construction, as long as the above homeomorphisms are understood.
Accordingly, we may write
for iterated product topological spaces without putting parenthesis.
The following are a sequence of examples all of the form that an abstractly constructed topological space is homeomorphic to a certain subspace of a Euclidean space. These examples are going to be useful in further developments below, for example in the proof below of the Heine-Borel theorem (prop. ).
-
Products of intervals are homeomorphic to hypercubes (example ).
-
The closed interval glued at its endpoints is homeomorphic to the circle (example ).
-
The cylinder, the Möbius strip and the torus are all homeomorphic to quotients of the square (example ).
Example
(product of closed intervals homeomorphic to hypercubes)
Let , and let for be closed intervals in the real line (example ), regarded as topological subspaces of the 1-dimensional Euclidean space (example ) with its metric topology (example ). Then the product topological space (def. , example ) of all these intervals is homeomorphic (def. ) to the corresponding topological subspace of the -dimensional Euclidean space (example ):
Similarly for open intervals:
Proof
There is a canonical bijection between the underlying sets. It remains to see that this, as well and its inverse, are continuous functions. For this it is sufficient to see that under this bijection the defining basis (def. ) for the product topology is also a basis for the subspace topology. But this is immediate from lemma .
Example
(closed interval glued at endpoints homeomorphic circle)
As topological spaces, the closed interval (def. ) with its two endpoints identified is homeomorphic (def. ) to the standard circle:
More in detail: let
be the unit circle in the plane
equipped with the subspace topology (example ) of the plane , which is itself equipped with its standard metric topology (example ).
Moreover, let
be the quotient topological space (example ) obtained from the interval with its subspace topology by applying the equivalence relation which identifies the two endpoints (and nothing else).
Consider then the function
given by
This has the property that , so that it descends to the quotient topological space
We claim that is a homeomorphism (definition ).
First of all it is immediate that is a continuous function. This follows immediately from the fact that is a continuous function and by definition of the quotient topology (example ).
So we need to check that has a continuous inverse function. Clearly the restriction of itself to the open interval has a continuous inverse. It fails to have a continuous inverse on and on and fails to have an inverse at all on [0,1], due to the fact that . But the relation quotiented out in is exactly such as to fix this failure.
Example
(cylinder, Möbius strip and torus homeomorphic to quotients of the square)
The square with two of its sides identified is the cylinder, and with also the other two sides identified is the torus:
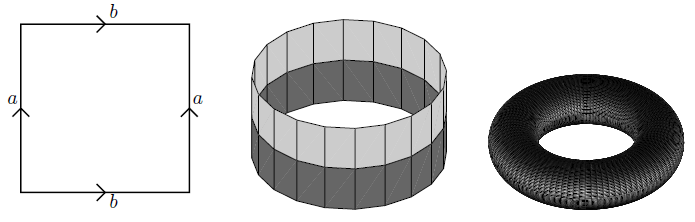
If the sides are identified with opposite orientation, the result is the Möbius strip:
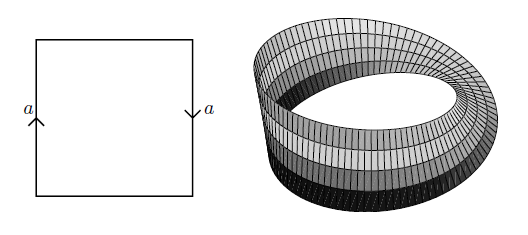
graphics grabbed from Lawson 03
Example
For then there is a homeomorphism (def. ) between the n-sphere (example ) with one point removed and the -dimensional Euclidean space (example ) with its metric topology (example ):
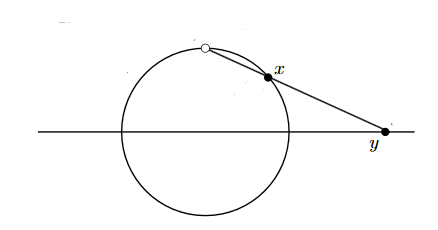
This homeomorphism is given by “stereographic projection”: One thinks of both the -sphere as well as the Euclidean space as topological subspaces (example ) of in the standard way (example ), such that they intersect in the equator of the -sphere. For one of the corresponding poles, then the homeomorphism is the function which sends a point along the line connecting it with to the point where this line intersects the equatorial plane.
In the canonical ambient coordinates this stereographic projection is given as follows:
Proof
First consider more generally the stereographic projection
of the entire ambient space minus the point onto the equatorial plane, still given by mapping a point to the unique point on the equatorial hyperplane such that the points , any sit on the same straight line.
This condition means that there exists such that
Since the only condition on is that this implies that
This equation has a unique solution for given by
and hence it follow that
Since rational functions are continuous (example ), this function is continuous and since the topology on is the subspace topology under the canonical embedding it follows that the restriction
is itself a continuous function (because its pre-images are the restrictions of the pre-images of to ).
To see that is a bijection of the underlying sets we need to show that for every
there is a unique satisfying
-
, hence
-
;
-
;
-
-
.
The last condition uniquely fixes the in terms of the given and the remaining , as
With this, the second condition says that
hence equivalently that
By the quadratic formula the solutions of this equation are
The solution violates the first condition above, while the solution satisfies it.
Therefore we have a unique solution, given by
In particular therefore also an inverse function to the stereographic projection exists and is a rational function, hence continuous by example . So we have exhibited a homeomorphism as required.
Important examples of pairs of spaces that are not homeomorphic include the following:
Theorem
(topological invariance of dimension)
For but , then the Euclidean spaces and (example , example ) are not homeomorphic.
More generally, an open subset in is never homeomorphic to an open subset in if .
The proofs of theorem are not elementary, in contrast to how obvious the statement seems to be intuitively. One approach is to use tools from algebraic topology: One assigns topological invariants to topological spaces, notably classes in ordinary cohomology or in topological K-theory), quantities that are invariant under homeomorphism, and then shows that these classes coincide for and for precisely only if .
One indication that topological invariance of dimension is not an elementary consequence of the axioms of topological spaces is that a related “intuitively obvious” statement is in fact false: One might think that there is no surjective continuous function if . But there are: these are called the Peano curves.
Separation axioms
The plain definition of topological space (above) happens to admit examples where distinct points or distinct subsets of the underlying set appear as more-or-less unseparable as seen by the topology on that set.
The extreme class of examples of topological spaces in which the open subsets do not distinguish distinct underlying points, or in fact any distinct subsets, are the codiscrete spaces (example ). This does occur in practice:
Example
(real numbers quotiented by rational numbers)
Consider the real line regarded as the 1-dimensional Euclidean space (example ) with its metric topology (example ) and consider the equivalence relation on which identifies two real numbers if they differ by a rational number:
Then the quotient topological space (def. )
is a codiscrete topological space (def. ), hence its topology does not distinguish any distinct proper subsets.
Here are some less extreme examples:
Example
(open neighbourhoods in the Sierpinski space)
Consider the Sierpinski space from example , whose underlying set consists of two points , and whose open subsets form the set . This means that the only (open) neighbourhood of the point is the entire space. Incidentally, also the topological closure of (def. ) is the entire space.
Example
Consider the disjoint union space (example ) of two copies of the real line regarded as the 1-dimensional Euclidean space (example ) with its metric topology (example ), which is equivalently the product topological space (example ) of with the discrete topological space on the 2-element set (example ):
Moreover, consider the equivalence relation on the underlying set which identifies every point in the th copy of with the corresponding point in the other, the th copy, except when :

The quotient topological space by this equivalence relation (def. )
is called the line with two origins. These “two origins” are the points and .
We claim that in this space every neighbourhood of intersects every neighbourhood of .
Because, by definition of the quotient space topology, the open neighbourhoods of are precisely those that contain subsets of the form
But this means that the “two origins” and may not be separated by neighbourhoods, since the intersection of with is always non-empty:
In many applications one wants to exclude at least some such exotic examples of topological spaces from the discussion and instead concentrate on those examples for which the topology recognizes the separation of distinct points, or of more general disjoint subsets. The relevant conditions to be imposed on top of the plain axioms of a topological space are hence known as separation axioms which we discuss in the following.
These axioms are all of the form of saying that two subsets (of certain kinds) in the topological space are ‘separated’ from each other in one sense if they are ‘separated’ in a (generally) weaker sense. For example the weakest axiom (called ) demands that if two points are distinct as elements of the underlying set of points, then there exists at least one open subset that contains one but not the other.
In this fashion one may impose a hierarchy of stronger axioms. For example demanding that given two distinct points, then each of them is contained in some open subset not containing the other () or that such a pair of open subsets around two distinct points may in addition be chosen to be disjoint (). Below in Tn-spaces we discuss the following hierarchy:
the main separation axioms
| number | name | statement | reformulation |
|---|---|---|---|
| Kolmogorov | given two distinct points, at least one of them has an open neighbourhood not containing the other point | every irreducible closed subset is the closure of at most one point | |
| given two distinct points, both have an open neighbourhood not containing the other point | all points are closed | ||
| Hausdorff | given two distinct points, they have disjoint open neighbourhoods | the diagonal is a closed map | |
| and… | all points are closed and… | ||
| regular Hausdorff | …given a point and a closed subset not containing it, they have disjoint open neighbourhoods | …every neighbourhood of a point contains the closure of an open neighbourhood | |
| normal Hausdorff | …given two disjoint closed subsets, they have disjoint open neighbourhoods | …every neighbourhood of a closed set also contains the closure of an open neighbourhood … every pair of disjoint closed subsets is separated by an Urysohn function |
The condition, , also called the Hausdorff condition is the most common among all separation axioms. Historically this axiom was originally taken as part of the definition of topological spaces, and it is still often (but by no means always) considered by default.
However, there are respectable areas of mathematics that involve topological spaces where the Hausdorff axiom fails, but a weaker axiom is still satisfied, called sobriety. This is the case notably in algebraic geometry (schemes are sober) and in computer science (Vickers 89). These sober topological spaces are singled out by the fact that they are entirely characterized by their sets of open subsets with their union and intersection structure (as in def. ) and may hence be understood independently from their underlying sets of points. This we discuss further below.
| hierarchy of separation axioms |
|---|
All separation axioms are satisfied by metric spaces (example , example below), from whom the concept of topological space was originally abstracted above. Hence imposing some of them may also be understood as gauging just how far one allows topological spaces to generalize away from metric spaces
spaces
There are many variants of separation axioms. The classical ones are labeled (for German “Trennungsaxiom”) with or higher. These we now introduce in def. and def. .
Definition
(the first three separation axioms)
Let be a topological space (def. ).
For any two points in the underlying set of which are not equal as elements of this set, consider the following propositions:

-
(T0) There exists a neighbourhood of one of the two points which does not contain the other point.
-
(T1) There exist neighbourhoods of both points which do not contain the other point.
-
(T2) There exists neighbourhoods_ of both points which do not intersect each other.
graphics grabbed from Vickers 89
The topological space is called a -topological space or just -space, for short, if it satisfies condition above for all pairs of distinct points.
A -topological space is also called a Kolmogorov space.
A -topological space is also called a Hausdorff topological space.
For definiteness, we re-state these conditions formally. Write for points in , write for open neighbourhoods of these points. Then:
-
(T0)
-
((T1)
-
(T2)
The following is evident but important:
Proposition
( are topological properties of increasing strength)
The separation properties from def. are topological properties in that if two topological spaces are homeomorphic (def. ) then one of them satisfies precisely if the other does.
Moreover, these properties imply each other as
Example
Examples of topological spaces that are not Hausdorff (def. ) include
-
the Sierpinski space (example ),
-
the line with two origins (example ),
-
the quotient topological space (example ).
Example
(finite -spaces are discrete)
For a finite topological space , hence one for which the underlying set is a finite set, the following are equivalent:
-
is a discrete topological space (def. ).
Example
(metric spaces are Hausdorff)
Every metric space (def ), regarded as a topological space via its metric topology (example ) is a Hausdorff topological space (def. ).
Because for two distinct points, then the distance between them is positive number, by the non-degeneracy axiom in def. . Accordingly the open balls (def. )
are disjoint open neighbourhoods.
Example
(subspace of -space is )
Let be a topological space satisfying the separation axiom for some according to def. . Then also every topological subspace (example ) satisfies .
(Beware that this fails for some higher discussed below in def. . Open subspaces of normal spaces need not be normal.)
Separation in terms of topological closures
The conditions , and have the following equivalent formulation in terms of topological closures (def. ).
Proposition
( in terms of topological closures)
A topological space is (def. ) precisely if the function that forms topological closures (def. ) of singleton subsets from the underlying set of to the set of irreducible closed subsets of (def. , which is well defined according to example ), is injective:
Proof
Assume first that is . Then we need to show that if are such that then . Hence assume that . Since the closure of a point is the complement of the union of the open subsets not containing the point (lemma ), this means that the union of open subsets that do not contain is the same as the union of open subsets that do not contain :
But if the two points were distinct, , then by one of the above unions would contain or , while the other would not, in contradiction to the above equality. Hence we have a proof by contradiction.
Conversely, assume that , and assume that . Hence by contraposition . We need to show that there exists an open set which contains one of the two points, but not the other.
Assume there were no such open subset, hence that every open subset containing one of the two points would also contain then other. Then by lemma this would mean that and that . But this would imply that and that , hence that . This is a proof by contradiction.
Proposition
( in terms of topological closures)
A topological space is (def. ) precisely if all its points are closed points (def. ).
Proof
We have
Here the first step is the reformulation of closure from lemma , the second is another application of the de Morgan law (prop. ), the third is the definition of union and complement, and the last one is manifestly by definition of .
Proposition
( in terms of topological closures)
A topological space is =Hausdorff precisely if the image of the diagonal
is a closed subset in the product topological space .
Proof
Observe that the Hausdorff condition is equivalently rephrased in terms of the product topology as: Every point which is not on the diagonal has an open neighbourhood which still does not intersect the diagonal, hence:
Therefore if is Hausdorff, then the diagonal is the complement of a union of such open sets, and hence is closed:
Conversely, if the diagonal is closed, then (by lemma ) every point not on the diagonal, hence with , has an open neighbourhood still not intersecting the diagonal, hence so that . Thus is Hausdorff.
Further separation axioms
Clearly one may and does consider further variants of the separation axioms , and from def. . Here we discuss two more:
Definition
Let be topological space (def. ).
Consider the following conditions
-
(T3) The space is (def. ) and for a point and a closed subset (def. ) not containing , then there exist disjoint open neighbourhoods and .
-
(T4) The space is (def. ) and for two disjoint closed subsets (def. ) then there exist disjoint open neighbourhoods .
If satisfies it is said to be a -space also called a regular Hausdorff topological space.
If satisfies it is to be a -space also called a normal Hausdorff topological space.
Example
(metric spaces are normal Hausdorff)
Let be a metric space (def. ) regarded as a topological space via its metric topology (example ). Then this is a normal Hausdorff space (def. ).
Proof
By example metric spaces are , hence in particular . What we need to show is that given two disjoint closed subsets then their exists disjoint open neighbourhoods and .
Recall the function
computing distances from a subset (example ). Then the unions of open balls (def. )
and
have the required properties.
Observe that:
Proposition
( are topological properties of increasing strength)
The separation axioms from def. , def. are topological properties (def. ) which imply each other as
Proof
The implications
and
are immediate from the definitions. The remaining implication follows with prop. : This says that by assumption of then all points in are closed, and with this the condition is manifestly a special case of the condition for .
Hence instead of saying “ is and …” one could just as well phrase the conditions and as “ is and …”, which would render the proof of prop. even more trivial.
The following shows that not every -space/Hausdorff space is /regular
Example
(K-topology)
Write
for the subset of natural fractions inside the real numbers.
Define a topological basis on consisting of all the open intervals as well as the complements of inside them:
The topology which is generated from this topological basis is called the K-topology.
We may denote the resulting topological space by
This is a Hausdorff topological space (def. ) which is not a regular Hausdorff space, hence (by prop. ) in particular not a normal Hausdorff space (def. ).
Further separation axioms in terms of topological closures
As before we have equivalent reformulations of the further separation axioms.
Proposition
( in terms of topological closures)
A topological space is a regular Hausdorff space (def. ), precisely if all points are closed and for all points with open neighbourhood there exists a smaller open neighbourhood whose topological closure is still contained in :
The proof of prop. is the direct specialization of the following proof for prop. to the case that (using that by , which is part of the definition of , the singleton subset is indeed closed, by prop. ).
Proposition
( in terms of topological closures)
A topological space is normal Hausdorff space (def. ), precisely if all points are closed and for all closed subsets with open neighbourhood there exists a smaller open neighbourhood whose topological closure is still contained in :
Proof
In one direction, assume that is normal, and consider
It follows that the complement of the open subset is closed and disjoint from :
Therefore by assumption of normality of , there exist open neighbourhoods with
But this means that
and since the complement of the open set is closed, it still contains the closure of , so that we have
as required.
In the other direction, assume that for every open neighbourhood of a closed subset there exists a smaller open neighbourhood with
Consider disjoint closed subsets
We need to produce disjoint open neighbourhoods for them.
From their disjointness it follows that
is an open neighbourhood. Hence by assumption there is an open neighbourhood with
Thus
are two disjoint open neighbourhoods, as required.
But the /normality axiom has yet another equivalent reformulation, which is of a different nature, and will be important when we discuss paracompact topological spaces below:
The following concept of Urysohn functions is another approach of thinking about separation of subsets in a topological space, not in terms of their neighbourhoods, but in terms of continuous real-valued “indicator functions” that take different values on the subsets. This perspective will be useful when we consider paracompact topological spaces below.
But the Urysohn lemma (prop. below) implies that this concept of separation is in fact equivalent to that of normality of Hausdorff spaces.
Definition
Let be a topological space, and let be disjoint closed subsets. Then an Urysohn function separating from is
to the closed interval equipped with its Euclidean metric topology (example , example ), such that
-
it takes the value 0 on and the value 1 on :
Proposition
Let be a normal Hausdorff topological space (def. ), and let be two disjoint closed subsets of . Then there exists an Urysohn function separating from (def. ).
Remark
Beware, the Urysohn function in prop. may take the values 0 or 1 even outside of the two subsets. The condition that the function takes value 0 or 1, respectively, precisely on the two subsets corresponds to “perfectly normal spaces”.
Proof
of Urysohn's lemma, prop.
Set
Since by assumption
we have
That is normal implies, by lemma , that every open neighbourhood of a closed subset contains a smaller neighbourhood together with its topological closure
Apply this fact successively to the above situation to obtain the following infinite sequence of nested open subsets and closed subsets
and so on, labeled by the dyadic rational numbers within
with the property
Define then the function
to assign to a point the infimum of the labels of those open subsets in this sequence that contain :
Here the limit is over the directed set of those that contain , ordered by reverse inclusion.
This function clearly has the property that and . It only remains to see that it is continuous.
To this end, first observe that
Here it is immediate from the definition that and that . For the remaining implication, it is sufficient to observe that
where is the boundary of .
This holds because the dyadic numbers are dense in . (And this would fail if we stopped the above decomposition into -s at some finite .) Namely, in one direction, if then for every small positive real number there exists a dyadic rational number with , and by construction hence . This implies that .
Now we claim that for all then
Thereby and are exhibited as unions of open subsets, and hence they are open.
Regarding the first point:
and
Regarding the second point:
and
(In these derivations we repeatedly use that is dense in (def. ), and we use the contrapositions of and .)
Now since the subsets form a sub-base (def. ) for the Euclidean metric topology on , it follows that all pre-images of are open, hence that is continuous.
As a corollary of Urysohn's lemma we obtain yet another equivalent reformulation of the normality of topological spaces, this one now of a rather different character than the re-formulations in terms of explicit topological closures considered above:
Proposition
(normality equivalent to existence of Urysohn functions)
A -space (def. ) is normal (def. ) precisely if it admits Urysohn functions (def ) separating every pair of disjoint closed subsets.
Proof
In one direction this is the statement of the Urysohn lemma, prop. .
In the other direction, assume the existence of Urysohn functions (def. ) separating all disjoint closed subsets. Let be disjoint closed subsets, then we need to show that these have disjoint open neighbourhoods.
But let be an Urysohn function with and then the pre-images
are disjoint open neighbourhoods as required.
reflection
While the topological subspace construction preserves the -property for (example ) the construction of quotient topological spaces in general does not, as shown by examples and .
Further below we will see that, generally, among all universal constructions in the category Top of all topological spaces those that are limits preserve the property, while those that are colimits in general do not.
But at least for , and there is a universal way, called reflection (prop. below), to approximate any topological space “from the left” by a topological spaces
Hence if one wishes to work within the full subcategory of the -spaces among all topological space, then the correct way to construct quotients and other colimits (see below) is to first construct them as usual quotient topological spaces (example ), and then apply the -reflection to the result.
Proposition
(-reflection)
Let . Then for every topological space there exists
-
a -topological space
-
called the -reflection of ,
which is the “closest approximation from the left” to by a -topological space, in that for any -space, then continuous functions of the form
are in bijection with continuous function of the form
and such that the bijection is constituted by
-
For this is known as the Kolmogorov quotient construction (see prop. below).
-
For this is known as Hausdorff reflection or Hausdorffication or similar.
Moreover, the operation extends to continuous functions
such as to preserve composition of functions as well as identity functions:
Finally, the comparison map is compatible with this in that
We prove this via a concrete construction of -reflection in prop. below. But first we pause to comment on the bigger picture of the -reflection:
Remark
In the language of category theory (remark ) the -reflection of prop. says that
-
is a functor from the category Top of topological spaces to the full subcategory of Hausdorff topological spaces;
-
is a natural transformation from the identity functor on Top to the functor
-
-topological spaces form a reflective subcategory of all topological spaces in that is left adjoint to the inclusion functor ; this situation is denoted as follows:
Generally, an adjunction between two functors
is for all pairs of objects , a bijection between sets of morphisms of the form
i.e.
and such that these bijections are “natural” in that they for all pairs of morphisms and then the folowing diagram commutes:
One calls the image under of the identity morphism the unit of the adjunction, written
One may show that it follows that the image under of a general morphism (called the adjunct of ) is given by this composite:
In the case of the reflective subcategory inclusion of the category of -spaces into the category Top of all topological spaces this adjunction unit is precisely the -reflection (only that we originally left the re-embedding notationally implicit).
There are various ways to see the existence and to construct the -reflections. The following is the quickest way to see the existence, even though it leaves the actual construction rather implicit.
Proposition
(-reflection via explicit quotients)
Let . Let be a topological space and consider the equivalence relation on the underlying set for which precisely if for every surjective continuous function into any -topological space (def. ) we have :
Then
-
the set of equivalence classes
equipped with the quotient topology (example ) is a -topological space,
-
the quotient projection
Proof
First we observe that every continuous function into a -topological space factors uniquely, via through a continuous function (this makes use of the “universal property” of the quotient topology, which we dwell on a bit more below in example ):
Clearly this continuous function is unique if it exists, because its underlying function of sets must be given by
First observe that this is indeed well defined as a function of underlying sets. To that end, factor through its image
equipped with its subspace topology as a subspace of (example ). By prop. also the image is a -topological space, since is. This means that if two elements have the same equivalence class, then, by definition of the equivalence relation, they have the same image under all continuous surjective functions into a -space, hence in particular they have the same image under :
This shows that is well defined as a function between sets.
To see that is also continuous, consider an open subset. We need to show that the pre-image is open in . But by definition of the quotient topology (example ), this is open precisely if its pre-image under the quotient projection is open, hence precisely if
is open in . But this is the case by the assumption that is continuous. Hence is indeed the unique continuous function as required.
What remains to be seen is that as constructed is indeed a -topological space. Hence assume that are two distinct points. Depending on the value of , need to produce open neighbourhoods around one or both of these points not containing the other point and possibly disjoint to each other.
Now by definition of the assumption means that there exists a -topological space and a surjective continuous function such that :
Accordingly, since is , there exist the respective kinds of neighbourhoods around and in . Moreover, by the previous statement there exists the continuous function with and . By the nature of continuous functions, the pre-images of these open neighbourhoods in are still open in and still satisfy the required disjunction properties. Therefore is a -space.
Here are alternative constructions of the reflections:
Proposition
Let be a topological space. Consider the relation on the underlying set by which precisely if neither has an open neighbourhood not containing the other. This is an equivalence relation. The quotient topological space by this equivalence relation (def. ) exhibits the -reflection of according to prop. .
A more explicit construction of the Hausdorff quotient than given by prop. is rather more involved. The issue is that the relation “ and are not separated by disjoint open neighbourhoods” is not transitive;
Proposition
(more explicit Hausdorff reflection)
For a topological space, write for the transitive closure of the relation given by the topological closure of the image of the diagonal .
Now for a topological space, define by induction for each ordinal number an equivalence relation on as follows, where we write for the corresponding quotient topological space projection:
We start the induction with the trivial equivalence relation:
- ;
For a successor ordinal we set
and for a limit ordinal we set
- .
Then:
A detailed proof is spelled out in (vanMunster 14, section 4).
Example
(Hausdorff reflection of the line with two origins)
The Hausdorff reflection (-reflection, prop. )
of the line with two origins from example is the real line itself:
Sober spaces
While the original formulation of the separation axioms from def. and def. clearly does follow some kind of pattern, its equivalent reformulation in terms of closure conditions in prop. , prop. , prop , prop. and prop. suggests rather different patterns. Therefore it is worthwhile to also consider separation-like axioms that are not among the original list.
In particular, the alternative characterization of the -condition in prop. immediately suggests the following strengthening, different from the -condition (see example below):
Definition
A topological space is called a sober topological space precisely if every irreducible closed subspace (def. ) is the topological closure (def. ) of a unique point, hence precisely if the function
from the underlying set of to the set of irreducible closed subsets of (def. , well defined according to example ) is bijective.
Proposition
Every Hausdorff topological space (def. ) is a sober topological space (def. ).
More specifically, in a Hausdorff topological space the irreducible closed subspaces (def. ) are precisely the singleton subspaces (def. ).
Hence, by example , in particular every metric space with its metric topology (example ) is sober.
Proof
The second statement clearly implies the first. To see the second statement, suppose that is an irreducible closed subspace which contained two distinct points . Then by the Hausdorff property there would be disjoint neighbourhoods , and hence it would follow that the relative complements and were distinct closed proper subsets of with
in contradiction to the assumption that is irreducible.
This proves by contradiction that every irreducible closed subset is a singleton. Conversely, generally the topological closure of every singleton is irreducible closed, by example .
By prop. and prop. we have the implications on the right of the following diagram:
| separation axioms |
|---|
But there there is no implication betwee and sobriety:
Proposition
The intersection of the classes of sober topological spaces (def. ) and -topological spaces (def. ) is not empty, but neither class is contained within the other.
That the intersection is not empty follows from prop. . That neither class is contained in the other is shown by the following counter-examples:
Example
( neither implies nor is implied by sobriety)
-
The Sierpinski space (def. ) is sober, but not .
-
The cofinite topology (example ) on a non-finite set is but not sober.
Finally, sobriety is indeed strictly weaker that Hausdorffness:
Example
(schemes are sober but in general not Hausdorff)
The Zariski topology on an affine space (example ) or more generally on the prime spectrum of a commutative ring (example ) is
For details see at Zariski topology this prop and this example.
Frames of opens
What makes the concept of sober topological spaces special is that for them the concept of continuous functions may be expressed entirely in terms of the relations between their open subsets, disregarding the underlying set of points of which these opens are in fact subsets.
Recall from example that for every continuous function the pre-image function is a frame homomorphism (def. ).
For sober topological spaces the converse holds:
Proposition
If and are sober topological spaces (def. ), then for every frame homomorphism (def. )
there is a unique continuous function such that is the function of forming pre-images under :
Proof
We first consider the special case of frame homomorphisms of the form
and show that these are in bijection to the underlying set , identified with the continuous functions via example .
By prop. , the frame homomorphisms are identified with the irreducible closed subspaces of . Therefore by assumption of sobriety of there is a unique point with . In particular this means that for an open neighbourhood of , then is not a subset of , and so it follows that . In conclusion we have found a unique such that
This is precisely the inverse image function of the continuous function which sends .
Hence this establishes the bijection between frame homomorphisms of the form and continuous functions of the form .
With this it follows that a general frame homomorphism of the form defines a function of sets by composition:
By the previous analysis, an element is sent to under this composite precisely if the corresponding point is in , and similarly for an element . It follows that is precisely that subset of points in which are sent by to elements of , hence that is the pre-image function of . Since by definition sends open subsets of to open subsets of , it follows that is indeed a continuous function. This proves the claim in generality.
Remark
(locales)
Proposition is often stated as saying that sober topological spaces are equivalently the “locales with enough points” (Johnstone 82, II 1.). Here “locale” refers to a concept akin to topological spaces where one considers just a “frame of open subsets” , without requiring that its elements be actual subsets of some ambient set. The natural notion of homomorphism between such generalized topological spaces are clearly the frame homomorphisms from def. .
From this perspective, prop. says that sober topological spaces are entirely characterized by their frames of opens and just so happen to “have enough points” such that these are actual open subsets of some ambient set, namely of .
Sober reflection
We saw above in prop. that every -topological space for has a “best approximation from the left” by a -topological space (for : “Hausdorff reflection”). We now discuss the analogous statement for sober topological spaces.
Recall again the point topological space (example ).
Definition
Let be a topological space.
Define to be the set
of frame homomorphisms (def. ) from the frame of opens of to that of the point. Define a topology on this set by declaring it to have one element for each element and given by
Consider the function
which sends an element to the function which assigns inverse images of the constant function on that element.
We are going to call this function the sober reflection of .
Lemma
(sober reflection is well defined)
The construction in def. is a topological space, and the function is a continuous function
Proof
To see that is closed under arbitrary unions and finite intersections, observe that the function
in fact preserves arbitrary unions and finite intersections. With this the statement follows by the fact that is closed under these operations.
To see that indeed preserves unions, observe that (e.g. Johnstone 82, II 1.3 Lemma)
where we used that the frame homomorphism preserves unions. Similarly for intersections, now with a finite set:
where we used that the frame homomorphism preserves finite intersections.
To see that is continuous, observe that , by construction.
Lemma
(sober reflection detects and sobriety)
For a topological space, the function from def. is
-
an injection precisely if is (def. );
-
a bijection precisely if is sober (def. ), in which case is in fact a homeomorphism (def. ).
Proof
By lemma there is an identification and via this is identified with the map .
Hence the second statement follows by definition, and the first statement by prop. .
That in the second case is in fact a homeomorphism follows from the definition of the opens : they are identified with the opens in this case (…expand…).
Lemma
(soberification lands in sober spaces, e.g. Johnstone 82, lemma II 1.7)
For a topological space, then the topological space from def. , lemma is sober.
Proof
Let be an irreducible closed subspace of . We need to show that it is the topological closure of a unique element .
Observe first that also is irreducible.
To see this use prop. , saying that irreducibility of is equivalent to . But if then also (as in the proof of lemma ) and hence by assumption on it follows that or . By lemma this in turn implies or . In conclusion, this shows that also is irreducible .
By lemma this irreducible closed subspace corresponds to a point . By that same lemma, this frame homomorphism takes the value on all those opens which are inside . This means that the topological closure of this point is just .
This shows that there exists at least one point of which is the topological closure. It remains to see that there is no other such point.
So let be two distinct points. This means that there exists with . Equivalently this says that contains one of the two points, but not the other. This means that is T0. By prop. this is equivalent to there being no two points with the same topological closure.
Proposition
(unique factorization through soberification)
For any topological space, for a sober topological space, and for a continuous function, then it factors uniquely through the soberification from def. , lemma
Proof
By the construction in def. , we find that the outer part of the following square commutes:
By lemma and lemma , the right vertical morphism is an isomorphism (a homeomorphism), hence has an inverse morphism. This defines the diagonal morphism, which is the desired factorization.
To see that this factorization is unique, consider two factorizations and apply the soberification construction once more to the triangles
Here on the right we used again lemma to find that the vertical morphism is an isomorphism, and that and do not change under soberification, as they already map between sober spaces. But now that the left vertical morphism is an isomorphism, the commutativity of this triangle for both and implies that .
In summary we have found
As before for the -reflection in remark , the statement of prop. may neatly be re-packaged:
Remark
(sober topological spaces are a reflective subcategory)
In the language of category theory (remark ) and in terms of the concept of adjoint functors (remark ), proposition simply says that sober topological spaces form a reflective subcategory of the category Top of all topological spaces
Universal constructions
We have seen above various construction principles for topological spaces above, such as topological subspaces and topological quotient spaces. It turns out that these constructions enjoy certain “universal properties” which allow us to find continuous functions into or out of these spaces, respectively (examples , example and below).
Since this is useful for handling topological spaces (we secretly used the universal property of the quotient space construction already in the proof of prop. ), we next consider, in def. below, more general “universal constructions” of topological spaces, called limits and colimits of topological spaces (and to be distinguished from limits in topological spaces, in the sense of convergence of sequences as in def. ).
Moreover, we have seen above that the quotient space construction in general does not preserve the -separation property or sobriety property of topological spaces, while the topological subspace construction does. The same turns out to be true for the more general “colimiting” and “limiting” universal constructions. But we have also seen that we may universally “reflect” any topological space to becomes a -space or sober space. The remaining question then is whether this reflection breaks the desired universal property. We discuss that this is not the case, that instead the universal construction in all topological spaces followed by these reflections gives the correct universal constructions in -separated and sober topological spaces, respectively (remark below).
After these general considerations, we finally discuss a list of examples of universal constructions in topological spaces.
To motivate the following generalizations, first observe the universal properties enjoyed by the basic construction principles of topological spaces from above
Example
(universal property of binary product topological space)
Let be topological spaces. Consider their product topological space from example . By example the two projections out of the product space are continuous functions
Now let be any other topological space. Then, by composition, every continuous function into the product space yields two continuous component functions and :
But in fact these two components completely characterize the function into the product: There is a (natural) bijection between continuous functions into the product space and pairs of continuous functions into the two factor spaces:
Example
(universal property of disjoint union spaces)
Let be topological spaces. Consider their disjoint union space from example . By definition, the two inclusions into the disjoint union space are clearly continuous functions
Now let be any other topological space. Then by composition a continuous function out of the disjoint union space yields two continuous component functions and :
But in fact these two components completely characterize the function out of the disjoint union: There is a (natural) bijection between continuous functions out of disjoint union spaces and pairs of continuous functions out of the two summand spaces:
Example
(universal property of quotient topological spaces)
Let be a topological space, and let be an equivalence relation on its underlying set. Then the corresponding quotient topological space together with the corresponding quotient continuous function has the following universal property:
Given any continuous function out of with the property that it respects the given equivalence relation, in that
then there is a unique continuous function such that
(We already made use of this universal property in the construction of the -reflection in the proof of prop. .)
Proof
First observe that there is a unique function as claimed on the level of functions of the underlying sets: In order for to hold, must send an equivalence class in to one of its members
and that this is well defined and independent of the choice of representative is guaranteed by the condition on above.
Hence it only remains to see that defined this way is continuous, hence that for an open subset, then its pre-image is open in the quotient topology. By definition of the quotient topology (example ), this is the case precisely if its further pre-image under is open in . But by the fact that , this is the case by the continuity of :
This kind of example we now generalize.
Limits and colimits
We consider now the general definition of free diagrams of topological spaces (def. below), their cones and co-cones (def. ) as well as limiting cones and colimiting cocones (def. below).
Then we use these concepts to see generally (remark below) why limits (such as product spaces and subspaces) of -spaces and of sober spaces are again or sober, respectively, and to see that the correct colimits (such as disjoint union spaces and quotient spaces) of - or sober spaces are instead the -reflection (prop. ) or sober reflection (prop. ), respectively, of these colimit constructions performed in the context of unconstrained topological spaces.
Definition
(free diagram of sets/topological spaces)
A free diagram of sets or of topological spaces is
-
an indexed set of sets or of topological spaces, respectively;
-
for every pair of labels, a set of functions of continuous functions, respectively, between these.
Here is a list of basic and important examples of free diagrams
Example
(discrete diagram and empty diagram)
Let be any set, and for each let be the empty set.
The corresponding free diagrams (def. ) are simply a set of sets/topological spaces with no specified (continuous) functions between them. This is called a discrete diagram.
For example for the set with 3-elements, then such a diagram looks like this:
Notice that here the index set may be empty set, , in which case the corresponding diagram consists of no data. This is also called the empty diagram.
Definition
Let be the set with two elements, and consider the sets
The corresponding free diagrams (def. ) are called pairs of parallel morphisms. They may be depicted like so:
Example
Let the set with three elements, and set
The corresponding free diagrams (def. ) look like so:
These are called span diagrams.
Similarly, there is the cospan diagram of the form
Example
Let be the set of natural numbers and consider
The corresponding free diagrams (def. ) are called tower diagrams. They look as follows:
Similarly there are co-tower diagram
Definition
(cone over a free diagram)
Consider a free diagram of sets or of topological spaces (def. )
Then
-
a cone over this diagram is
-
a set or topological space (called the tip of the cone);
-
for each a function or continuous function
such that
-
for all and all then the condition
holds, which we depict as follows:
-
-
a co-cone over this diagram is
-
a set or topological space (called the tip of the co-cone);
-
for each a function or continuous function ;
such that
-
for all and all then the condition
holds, which we depict as follows:
-
Example
(solutions to equations are cones)
Let be two functions from the real numbers to themselves, and consider the corresponding parallel morphism diagram of sets (example ):
Then a cone (def. ) over this free diagram with tip the singleton set is a solution to the equation
Namely the components of the cone are two functions of the form
hence equivalently two real numbers, and the conditions on these are
Definition
(limiting cone over a diagram)
Consider a free diagram of sets or of topological spaces (def. ):
Then
-
its limiting cone (or just limit for short, also “inverse limit”, for historical reasons) is the cone
over this diagram (def. ) which is universal among all possible cones, in that for
any other cone, then there is a unique function or continuous function, respectively
that factors the given cone through the limiting cone, in that for all then
which we depict as follows:
-
its colimiting cocone (or just colimit for short, also “direct limit”, for historical reasons) is the cocone
under this diagram (def. ) which is universal among all possible co-cones, in that it has the property that for
any other cocone, then there is a unique function or continuous function, respectively
that factors the given co-cone through the co-limiting cocone, in that for all then
which we depict as follows:
We now briefly mention the names and comment on the general nature of the limits and colimits over the free diagrams from the list of examples above. Further below we discuss examples in more detail.
shapes of free diagrams and the names of their limits/colimits
Example
(initial object and terminal object)
Consider the empty diagram (def. ).
-
A cone over the empty diagram is just an object , with no further structure or condition. The universal property of the limit “” over the empty diagram is hence that for every object , there is a unique map of the form , with no further condition. Such an object is called a terminal object.
-
A co-cone over the empty diagram is just an object , with no further structure or condition. The universal property of the colimit “” over the empty diagram is hence that for every object , there is a unique map of the form . Such an object is called an initial object.
Example
(Cartesian product and coproduct)
Let be a discrete diagram (example ), i.e. just a set of objects.
-
The limit over this diagram is called the Cartesian product, denoted ;
-
The colimit over this diagram is called the coproduct, denoted .
Example
Let
be a free diagram of the shape “pair of parallel morphisms” (example ).
A limit over this diagram according to def. is also called the equalizer of the maps and . This is a set or topological space equipped with a map , so that and such that if is any other map with this property
then there is a unique factorization through the equalizer:
In example we have seen that a cone over such a pair of parallel morphisms is a solution to the equation .
The equalizer above is the space of all solutions of this equation.
Example
(pullback/fiber product and coproduct)
Consider a cospan diagram (example )
The limit over this diagram is also called the fiber product of with over , and denoted . Thought of as equipped with the projection map to , this is also called the pullback of along
Dually, consider a span diagram (example )
The colimit over this diagram is also called the pushout of along , denoted :
Often the defining universal property of a limit/colimit construction is all that one wants to know. But sometimes it is useful to have an explicit description of the limits/colimits, not the least because this proves that these actually exist. Here is the explicit description of the (co-)limiting cone over a diagram of sets:
Proposition
Let
be a free diagram of sets (def. ). Then
-
its limit cone (def. ) is given by the following subset of the Cartesian product of all the sets appearing in the diagram
on those tuples of elements which match the graphs of the functions appearing in the diagram:
and the projection functions are .
-
its colimiting co-cone (def. ) is given by the quotient set of the disjoint union of all the sets appearing in the diagram
with respect to the equivalence relation which is generated from the graphs of the functions in the diagram:
and the injection functions are the evident maps to equivalence classes:
Proof
We discuss the proof of the first case. The second is directly analogous.
First observe that indeed, by construction, the projection maps as given do make a cone over the free diagram, by the very nature of the relation that is imposed on the tuples:
We need to show that this is universal, in that every other cone over the free diagram factors universally through this one. First consider the case that the tip of a given cone is a singleton:
As shown on the right, the data in such a cone is equivalently: for each an element , such that for all and then . But this is precisely the relation used in the construction of the limit above and hence there is a unique map
such that for all we have
namely that map is the one that picks the element .
This shows that every cone with tip a singleton factors uniquely through the claimed limiting cone. But then for a cone with tip an arbitrary set , this same argument applies to all the single elements of .
It will turn out below in prop. that limits and colimits of diagrams of topological spaces are computed by first applying prop. to the underlying diagram of underlying sets, and then equipping the result with a topology as follows:
Definition
(initial topology and final topology)
Let be a set of topological spaces, and let be a bare set. Then
-
For
a set of functions out of , the initial topology is the coarsest topology on (def. ) such that all are continuous.
By lemma this is equivalently the topology whose open subsets are the unions of finite intersections of the preimages of the open subsets of the component spaces under the projection maps, hence the topology generated from the sub-base
-
For
a set of functions into , the final topology is the finest topology on (def. ) such that all are continuous.
Hence a subset is open in the final topology precisely if for all then the pre-image is open.
Beware a variation of synonyms that is in use:
| limit topology | colimit topology |
|---|---|
| initial topology | final topology |
| weak topology | strong topology |
| coarse topology | fine topology |
We have already seen above simple examples of initial and final topologies:
Example
(subspace topology as an initial topology)
For a single topological space, and a subset of its underlying set, then the initial topology , def. , is the subspace topology from example , making
a topological subspace inclusion.
Example
(quotient topology as a final topology)
Conversely, for a topological space and for a surjective function out of its underlying set, then the final topology on , from def. , is the quotient topology from example , making a continuous function:
Now we have all the ingredients to explicitly construct limits and colimits of diagrams of topological spaces:
Proposition
(limits and colimits of topological spaces)
Let
be a free diagram of topological spaces (def. ).
-
The limit over this free diagram (def. ) is given by the topological space
-
whose underlying set is the limit of the underlying sets according to prop. ;
-
whose topology is the initial topology, def. , for the functions which are the limiting cone components:
Hence
-
-
The colimit over the free diagram (def. ) is the topological space
-
whose underlying set is the colimit of sets of the underlying diagram of sets according to prop. ,
-
whose topology is the final topology, def. for the component maps of the colimiting cocone
Hence
-
(e.g. Bourbaki 71, section I.4)
Proof
We discuss the first case, the second is directly analogous:
Consider any cone over the given free diagram:
By the nature of the limiting cone of the underlying diagram of underlying sets, which always exists by prop. , there is a unique function of underlying sets of the form
satisfying the required conditions . Since this is already unique on the underlying sets, it is sufficient to show that this function is always continuous with respect to the initial topology.
Hence let be in . By def. , this means that is a union of finite intersections of subsets of the form with open. But since taking pre-images preserves unions and intersections (prop. ), and since unions and intersections of opens in are again open, it is sufficient to consider of the form . But then by the condition that we find
and this is open by the assumption that is continuous.
We discuss a list of examples of (co-)limits of topological spaces in a moment below, but first we conclude with the main theoretical impact of the concept of topological (co-)limits for our our purposes.
Here is a key property of (co-)limits:
Proposition
(functions into a limit cone are the limit of the functions into the diagram)
Let be a free diagram (def. ) of sets or of topological spaces.
-
If the limit exists (def. ), then the set of (continuous) function into this limiting object is the limit over the sets of (continuous) functions (“homomorphisms”) into the components :
Here on the right we have the limit over the free diagram of sets given by the operations of post-composition with the maps in the original diagram:
-
If the colimit exists, then the set of (continuous) functions out of this colimiting object is the limit over the sets of morphisms out of the components of :
Here on the right we have the colimit over the free diagram of sets given by the operations of pre-composition with the original maps:
Proof
We give the proof of the first statement. The proof of the second statement is directly analogous (just reverse the direction of all maps).
First observe that, by the very definition of limiting cones, maps out of some into them are in natural bijection with the set of cones over the corresponding diagram with tip :
Hence it remains to show that there is also a natural bijection like so:
Now, again by the very definition of limiting cones, a single element in the limit on the right is equivalently a cone of the form
This is equivalently for each a choice of map , such that for each and we have . And indeed, this is precisely the characterization of an element in the set .
Using this, we find the following:
Remark
(limits and colimits in categories of nice topological spaces)
Recall from remark the concept of adjoint functors
witnessed by natural isomorphisms
Then these adjoints preserve (co-)limits in that
-
the left adjoint functor preserve colimits (def. )
in that for every diagram in there is a natural isomorphism of the form
-
the right adjoint functor preserve limits (def. )
in that for every diagram in there is a natural isomorphism of the form
This implies that if we have a reflective subcategory of topological spaces
(such as with -spaces according to remark or with sober spaces according to remark )
then
-
limits in are computed as limits in ;
-
colimits in are computed as the reflection of the colimit in .
For example let be a diagram of Hausdorff spaces, regarded as a diagram of general topological spaces. Then
-
not only is the limit of topological spaces according to prop. again a Hausdorff space, but it also satisfies its universal property with respect to the category of Hausdorff spaces;
-
not only is the reflection of the colimit as topological spaces a Hausdorff space (while the colimit as topological spaces in general is not), but this reflection does satisfy the universal property of a colimit with respect to the category of Hausdorff spaces.
Proof
First to see that right/left adjoint functors preserve limits/colimits: We discuss the case of the right adjoint functor preserving limits. The other case is directly analogous (just reverse the direction of all arrows).
So let be the limit over some diagram . To test what a right adjoint functor does to this, we may map any object into it. Using prop. this yields
Since this is true for all , it follows that
Now to see that limits/colimits in the reflective subcategory are computed as claimed;
(…)
Examples
We now discuss a list of examples of universal constructions of topological spaces as introduced in generality above.
examples of universal constructions of topological spaces:
Example
(empty space and point space as empty colimit and limit)
Consider the empty diagram (example ) as a diagram of topological spaces. By example the limit and colimit (def. ) over this type of diagram are the terminal object and initial object, respectively. Applied to topological spaces we find:
-
The limit of topological spaces over the empty diagram is the point space (example ).
-
The colimit of topological spaces over the empty diagram is the empty topological space (example ).
This is because for an empty diagram, the a (co-)cone is just a topological space, without any further data or properties, and it is universal precisely if there is a unique continuous function to (respectively from) this space to any other space . This is the case for the point space (respectively empty space) by example :
Example
(binary product topological space and disjoint union space as limit and colimit)
Consider a discrete diagram consisting of two topological spaces (example ). Generally, it limit and colimit is the product and coproduct , respectively (example ).
-
In topological space this product is the binary product topological space from example , by the universal property observed in example :
-
In topological spaces, this coproduct is the disjoint union space from example , by the universal property observed in example :
So far these examples just reproduces simple constructions which we already considered. Now the first important application of the general concept of limits of diagrams of topological spaces is the following example of product spaces with an non-finite set of factors. It turns out that the correct topology on the underlying infinite Cartesian product of sets is not the naive generalization of the binary product topology, but instead is the corresponding weak topology, which in this case is called the Tychonoff topology:
Example
(general product topological spaces with Tychonoff topology)
Consider an arbitrary discrete diagram of topological spaces (def. ), hence a set of topological spaces, indexed by any set , not necessarily a finite set.
The limit over this diagram (a Cartesian product, example ) is called the product topological space of the spaces in the diagram, and denoted
By prop. and prop. , the underlying set of this product space is just the Cartesian product of the underlying sets, hence the set of tuples . This comes for each with the projection map
By prop. and def. , the topology on this set is the coarsest topology such that the pre-images of open subsets under these projection maps are open. Now one such pre-image is a Cartesian product of open subsets of the form
The coarsest topology that contains these open subsets ist that generated by these subsets regarded as a sub-basis for the topology (def. ), hence the arbitrary unions of finite intersections of subsets of the above form.
Observe that a binary intersection of these generating open is (for ):
and generally for a finite subset then
Therefore the open subsets of the product topology are unions of those of this form. Hence the product topology is equivalently that generated by these subsets when regarded as a basis for the topology (def. ).
This is also known as the Tychonoff topology.
Notice the subtlety: Naively we could have considered as open subsets the unions of products of open subsets of the factors, without the constraint that only finitely many of them differ from the corresponding total space. This also defines a topology, called the box topology. For a finite index set the box topology coincides with the product space (Tychonoff) topology, but for non-finite it is strictly finer (def. ).
Example
Write for the the discrete topological space with two points (example ). Write for the product topological space (example ) of a countable set of copies of this discrete space with itself (i.e. thehight corresponding Cartesian product of sets equipped with the Tychonoff topology induced from the discrete topology of ).
Notice that due to the nature of the Tychonoff topology, this product space is not itself discrete.
Consider the function
which sends an element in the product space, hence a sequence of binary digits, to the value of the power series as shown on the right.
One checks that this is a continuous function (from the product topology to the Euclidean metric topology on the closed interval). Moreover with its image equipped with its subspace topology, then this is a homeomorphism onto its image:
This image is called the Cantor space.
Example
(equalizer of continuous functions)
The equalizer (example ) of two continuous functions is the equalizer of the underlying functions of sets
(hence the largest subset of on which both functions coincide) and equipped with the subspace topology from example .
Example
(coequalizer of continuous functions)
The coequalizer of two continuous functions is the coequalizer of the underlying functions of sets
(hence the quotient set by the equivalence relation generated by the relation for all ) and equipped with the quotient topology, example .
Example
(union of two open or two closed subspaces is pushout)
Let be a topological space and let be subspaces such that
-
are both open subsets or are both closed subsets;
-
they constitute a cover:
Write and for the corresponding inclusion continuous functions.
Then the commuting square
is a pushout square in Top (example ).
By the universal property of the pushout this means in particular that for any topological space then a function of underlying sets
is a continuous function as soon as its two restrictions
are continuous.
More generally if is a cover of by an arbitrary set of open subsets or by a finite set of closed subsets, then a function is continuous precisely if all its restrictions for are continuous.
Proof
By prop. the underlying diagram of underlying sets is clearly a pushout in Set. Therefore, by prop. , we need to show that the topology on is the final topology (def. ) induced by the set of functions , hence that a subset is an open subset precisely if the pre-images (restrictions)
are open subsets of and , respectively.
Now by definition of the subspace topology, if is open, then the intersections and are open in these subspaces.
Conversely, assume that and are open. We need to show that then is open.
Consider now first the case that are both open open. Then by the nature of the subspace topology, that is open in means that there is an open subset such that . Since the intersection of two open subsets is open, this implies that and hence is open. Similarly . Therefore
is the union of two open subsets and therefore open.
Now consider the case that are both closed subsets.
Again by the nature of the subspace topology, that and are open means that there exist open subsets such that and . Since are closed by assumption, this means that are still closed, hence that are open.
Now observe that (by de Morgan duality)
This exhibits as the intersection of two open subsets, hence as open.
Example
Consider a cospan diagram (example ) of continuous functions
The colimit under this diagram called the pushout (example )
Consider on the disjoint union set the equivalence relation generated by the relation
Then prop. implies that the pushout is equivalently the quotient topological space (example ) by this equivalence relation of the disjoint union space (example ) of and :
If is an topological subspace inclusion , then in topology its pushout along is traditionally written as
and called the attachment space (sometimes: attaching space or adjunction space) of along .
(graphics from Aguilar-Gitler-Prieto 02)
Example
(n-sphere as pushout of the equator inclusions into its hemispheres)
As an important special case of example , let
be the canonical inclusion of the standard (n-1)-sphere as the boundary of the standard n-disk (example ).
Then the colimit of topological spaces under the span diagram,
is the topological n-sphere (example ):
(graphics from Ueno-Shiga-Morita 95)
In generalization of this example, we have the following important concept:
Definition
(single cell attachment)
For any topological space and for , then an -cell attachment to is the result of gluing an n-disk to , along a prescribed image of its bounding (n-1)-sphere (def. ):
Let
be a continuous function, then the space attachment (example )
is the topological space which is the pushout of the boundary inclusion of the -sphere along , hence the universal space that makes the following diagram commute:
Example
(discrete topological spaces from 0-cell attachment to the empty space)
A single cell attachment of a 0-cell, according to example is the same as forming the disjoint union space with the point space :
In particular if we start with the empty topological space itself (example ), then by attaching 0-cells we obtain a discrete topological space. To this then we may attach higher dimensional cells.
Definition
(attaching many cells at once)
If we have a set of attaching maps (as in def. ), all to the same space , we may think of these as one single continuous function out of the disjoint union space of their domain spheres
Then the result of attaching all the corresponding -cells to is the pushout of the corresponding disjoint union of boundary inclusions:
Apart from attaching a set of cells all at once to a fixed base space, we may “attach cells to cells” in that after forming a given cell attachment, then we further attach cells to the resulting attaching space, and ever so on:
Definition
(relative cell complexes and CW-complexes)
Let be a topological space, then A topological relative cell complex of countable height based on is a continuous function
and a sequential diagram of topological space of the form
such that
-
each is exhibited as a cell attachment according to def. , hence presented by a pushout diagram of the form
-
is the union of all these cell attachments, and is the canonical inclusion; or stated more abstractly: the map is the inclusion of the first component of the diagram into its colimiting cocone :
If here is the empty space then the result is a map , which is equivalently just a space built form “attaching cells to nothing”. This is then called just a topological cell complex of countable height.
Finally, a topological (relative) cell complex of countable height is called a CW-complex is the -st cell attachment is entirely by -cells, hence exhibited specifically by a pushout of the following form:
Given a CW-complex, then is also called its -skeleton.
A finite CW-complex is one which admits a presentation in which there are only finitely many attaching maps, and similarly a countable CW-complex is one which admits a presentation with countably many attaching maps.
Subspaces
We discuss special classes of subspaces of topological spaces that play an important role in the theory, in particular for the discussion of topological manifolds below:
Connected components
Via homeomorphism to disjoint union spaces one may characterize whether topological spaces are connected (def. below), and one may decompose every topological space into its connected components (def. below).
The important subtlety in to beware of is that a topological space is not in general the disjoint union space of its connected components. The extreme case of this phenomenon are totally disconnected topological spaces (def. below) which are nevertheless not discrete (examples and below). Spaces which are free from this exotic behaviour include the locally connected topological spaces (def. below) and in particular the locally path-connected topological spaces (def. below).
Definition
A topological space (def. ) is called connected if the following equivalent conditions hold:
-
For all pairs of topological spaces such that is homeomorphic (def. ) to their disjoint union space (def. )
then exactly one of the two spaces is the empty space (example ).
-
For all pairs of open subsets if
then exactly one of the two subsets is the empty set;
-
if a subset is both an open subset and a closed subset (def. ) then if and only if is non-empty.
Proof
First consider the equivalence of the first two statements:
Suppose that in every disjoint union decomposition of exactly one summand is empty. Now consider two disjoint open subsets whose union is and whose intersection is empty. We need to show that exactly one of the two subsets is empty.
Write and for the corresponding topological subspaces. Then observe that from the definition of subspace topology (example ) and of the disjoint union space (example ) we have a homeomorphism
because by assumption every open subset is the disjoint union of open subsets of and , respectively:
which is the definition of the disjoint union topology.
Hence by assumption exactly one of the two summand spaces is the empty space and hence the underlying set is the empty set.
Conversely, suppose that for every pair of open subsets with and then exactly one of the two is empty. Now consider a homeomorphism of the form . By the nature of the disjoint union space this means that are disjoint open subsets of which cover . So by assumption precisely one of the two subsets is the empty set and hence precisely one of the two topological spaces is the empty space.
Now regarding the equivalence to the third statement:
If a subset is both closed and open, this means equivalently that it is open and that its complement is also open, hence equivalently that there are two open subsets whose union is and whose intersection is empty. This way the third condition is equivalent to the second, hence also to the first.
Remark
(empty space is not connected)
According to def. the empty topological space (def. ) is not connected, since , where both instead of exactly one of the summands are empty.
Of course it is immediate to change def. so that it would regard the empty space as connected. This is a matter of convention.
Example
(connected subspaces of the real line are the intervals)
Regard the real line with its Euclidean metric topology (example , ). Then a subspace (example ) is connected (def. ) precisely if it is an interval, hence precisely if
Proof
Suppose on the contrary that we had but . Then by the nature of the subspace topology there would be a decomposition of as a disjoint union of disjoint open subsets:
But since and both these open subsets were non-empty, thus contradicting the assumption that is connected. This yields a proof by contradiction.
Proposition
(continuous images of connected spaces are connected)
Let be a connected topological space (def. ), let be any topological space, and let
be a continuous function (def. ). This factors via continuous functions through the image
for equipped either with he subspace topology relative to or the quotient topology relative to (example ). In either case:
If is a connected topological space (def. ), then so is .
In particular connectedness is a topological property (def. ).
Proof
Let be two open subsets such that and . We need to show that precisely one of them is the empty set.
Since is a continuous function, also the pre-images are open subsets and are still disjoint. Since is surjective it also follows that . Since is connected, it follows that one of these two pre-images is the empty set. But again sicne is surjective, this implies that precisely one of is empty, which means that is connected.
This yields yet another quick proof via topology of a classical fact of analysis:
Corollary
Regard the real numbers with their Euclidean metric topology (example , example ), and consider a closed interval (example ) equipped with its subspace topology (example ).
Then a continuous function (def. )
takes every value in between and f(b).
Proof
By example the interval is connected. By prop. also its image is connected. By example that image is hence itself an interval. This implies the claim.
Example
(product space of connected spaces is connected)
Let be a set of connected topological spaces (def. ). Then also their product topological space (example ) is connected.
Proof
Let be an open cover of the product space by two disjoint open subsets. We need to show that precisely one of the two is empty. Since each is connected and hence non-empty, the product space is not empty, and hence it is sufficient to show that at least one of the two is empty.
Assume on the contrary that both and were non-empty.
Observe first that if so, then we could find and whose coordinates differed only in a finite subset of . This is since by the nature of the Tychonoff topology and for all but a finite number of .
Next observe that we then could even find that differed only in a single coordinate from : Because pick one coordinate in which differs from and change it to the corresponding coordinate of . Since and are a cover, the resulting point is either in or in . If it is in , then already differed in only one coordinate from and we may take . If instead the new point is in , then rename it to and repeat the argument. By induction this finally yields an as claimed.
Therefore it is now sufficient to see that it leads to a contradiction to assume that there are points and that differ in only the th coordinate, for some , in that this would imply that .
Observe that the inclusion
which is the identity on the th component and is otherwise constant on the th component of or equivalently of is a continuous function, by the nature of the Tychonoff topology (example ).
Therefore also the restrictions and are open subsets. Moreover they are still disjoint and cover . Hence by the connectedness of , precisely one of them is empty. This means that the -component of both and must be in the other subset of , and hence that and must both be in or both in , contrary to the assumption.
While topological spaces are not always connected, they always decompose at least as sets into their connected components:
Definition
For a topological space, then its connected components are the equivalence classes under the equivalence relation on which regards two points as equivalent if they both sit in some subset which, as a topological subspace (example ), is connected (def. ):
Equivalently, the connected components are the maximal elements in the pre-ordered set of connected subspaces, pre-ordered by inclusion.
Example
(connected components of disjoint union spaces)
For an -indexed set of connected topological spaces, then the set of connected components (def. ) of their disjoint union space (example ) is the index set .
In general the situation is more complicated than in example , this we come to in examples and below. But first notice some basic properties of connected components:
Proposition
(topological closure of connected subspace is connected)
Let be a topological space and let be a subset which, as a subspace, is connected (def. ). Then also the topological closure is connected
Proof
Suppose that with disjoint open subsets. We need to show that one of the two is empty.
But also the intersections are disjoint subsets, open as subsets of the subspace with . Hence by the connectedness of , one of or is empty. Assume is empty, otherwise rename. Hence , or equivalently: . By disjointness of and this means that . But since is open, is still closed, so that
This means that , and hence that is connected.
Proposition
(connected components are closed)
Let be a topological space. Then its connected components (def. ) are closed subsets.
Proof
By definition, the connected components are maximal elements in the set of connected subspaces pre-ordered by inclusion. Assume a connected component were not closed. By prop. its closure is still closed, and would be strictly larger, contradicting the maximality of . This yields a proof by contradiction.
Remark
Prop. implies that when a space has a finite set of connected components, then they are not just closed but also open, hence clopen subsets (because then each is the complement of a finite union of closed subspaces). This in turn means that the space is the disjoint union space of its connected components.
For a non-finite set of connected components this remains true if the space is locally connected see def. , lemma below.
We now highlight the subtlety that not every topological space is the disjoint union of its connected components. For this it is useful to consider the following extreme situation:
Definition
(totally disconnected topological space)
A topological space is called totally disconnected if all its connected components (def. ) are singletons, hence point spaces (example ).
The trivial class of examples is this:
Example
(discrete topological spaces are totally disconnected)
Every discrete topological space (example ) is a totally disconnected topological space (def. ).
But the important point is that there are non-discrete totally disconnected topological spaces:
Example
(the rational numbers are totally disconnected but non-discrete topological space)
The rational numbers equipped with their subspace topology (def. ) inherited from the Euclidean metric topology (example , example ) on the real numbers, form a totally disconnected space (def. ), but not a discrete topological space (example ).
Proof
It is clear that the subspace topology is not discrete, since the singletons are not open subsets (because their pre-image in are still singletons, and the points in a metric space are closed, by example and prop. ).
What we need to see is that is nevertheless totally disconnected:
By construction, a base for the topology (def. ) is given by the open subsets which are restrictions of open intervals of real numbers to the rational numbers
for .
Now for any such there exists an irrational number with . This being irrational implies that and are disjoint subsets. Therefore every basic open subset is the disjoint union of (at least) two open subsets:
Hence no non-empty open subspace of the rational numbers is connected.
Example
(Cantor space is totally disconnected but non-discrete)
The Cantor space (example ) is a totally disconnected topological space (def. ) but is not a discrete topological space.
Proof
The base opens (def. ) of the product topological space (example ) are of the form
First of all this is not the discrete topology, for that also contains infinite products of proper subsets of as open subsets, hence is strictly finer.
On the other hand, since is finite, is non-empty and hence there exists some such that the corresponding factor in the above product is the full set . But then the above subset is the disjoint union of the open subsets
In particular if are two distinct points in the original open subset, them being distinct means that there is a smallest such that they have different coordinates in in that position. By the above this implies that they belong to different connected components.
In applications to geometry (such as in the definition of topological manifolds below) one is typically interested in topological spaces which do not share the phenomenon of examples or , hence which are the disjoint union of their connected components:
Definition
(locally connected topological spaces)
A topological space is called locally connected if the following equivalent conditions hold:
-
For every point and every neighbourhood there is a connected (def. ) open neighbourhood .
-
Every connected component of every open subspace of is open.
-
Every open subspace (example ) is the disjoint union space (def. ) of its connected components (def. ).
Proof
1) 2)
Assume every neighbourhood of contains a connected neighbourhood and let be an open subset with a connected component. We need to show that is open.
Consider any point . Since then also , there is a connected open neighbourhood of in . Observe that this must be contained in , for if it were not then were a larger open connected open neighbourhood, contradicting the maximality of the connected component .
Hence is a union of open subsets, and hence itself open.
2) 3)
Now assume that every connected component of every open subset is open. Since the connected components generally constitute a cover of by disjoint subsets, this means that now they form an open cover by disjoint subsets. But by forming intersections with the cover this implies that every open subset of is the disjoint union of open subsets of the connected components (and of course every union of open subsets of the connected components is still open in ), which is the definition of the topology on the disjoint union space of the connected components.
3) 1)
Finally assume that every open subspace is the disjoint union of its connected components. Let be a point and a neighbourhood. We need to show that contains a connected neighbourhood of .
But, by definition, contains an open neighbourhood of and by assumption this decomposes as the disjoint union of its connected components. One of these contains . Since in a disjoint union space all summands are open, this is the required connected open neighbourhood.
Example
(Euclidean space is locally connected)
For the Euclidean space (example ) (with its metric topology, example ) is locally connected (def. ).
Proof
By nature of the Euclidean metric topology, every neighbourhood of a point contains an open ball containing (def. ). Moreover, every open ball clearly contains an open cube, hence a product space of open intervals which is still a neighbourhood of (example ).
Now intervals are connected by example and product spaces of connected spaces are connected by example . This shows that ever open neighbourhood contains a connected neighbourhood, which is the characterization of local connectedness in the first item of def. .
Proposition
(open subspace of locally connected space is locally connected)
Every open subspace (example ) of a locally connected topological space (example ) is itself locally connected
Another important class of examples of locally connected topological spaces are topological manifolds, this we discuss as prop. below.
There is also a concept of connectedness which is “geometric” instead of “purely topological” by definition:
Definition
(path)
Let be a topological space. Then a path or continuous curve in is a continuous function
from the closed interval (example ) equipped with its Euclidean metric topology (example , example ).
We say that this path connects its endpoints .
The following is obvious, but the construction is important:
Lemma
(being connected by a path is equivalence relation)
Let be a topological space. Being connected by a path (def. ) is an equivalence relation on the underlying set of points .
Proof
We need to show that the relation is reflexive, symmetric and transitive.
For a point, then the constant function with value
is continuous (example ). Therefore for all points (reflexivity).
For two points and
a path connecting them, then the reverse path
is continuous (the function is continuous because polynomials are continuous ). Hence with also (symmetry).
For three points and for
two paths with , and
consider the function
This is a continuous function by example , hence this constitutes a path connecting with (the “concatenated path”). Therefore and implies (transitivity).
Definition
Let be a topological space. The equivalence classes of the equivalence relation “connected by a path” (def. , lemma ) are called the path-connected components of . The set of the path-connected components is usually denoted
(The notation reflects the fact that this is the degree-zero case of a more general concept of homotopy groups for all . We discuss the fundamental group in part 2. The higher homotopy groups are discussed in Introduction to Homotopy Theory).
If there is a single path-connected component (), then is called a path-connected topological space.
Example
(Euclidean space is path-connected)
For then Euclidean space is a path-connected topological space (def. ).
Because for , consider the function
This clearly has the property that and . Moreover, it is a polynomial function and polynomials are continuous functions (example ).
Example
(continuous image of path-connected space is path-connected)
Let be a path-connected topological space and let
be a continuous function. Then also the image of
with either of its two possible topologies (example ) is path-connected.
In particular path-connectedness is a topological property (def. ).
Proof
Let be two points. Since is surjective, there are pre-images . Since is path-connected, there is a continuous function
with and . Since the composition of continuous functions is continuous, it follows that is a path connecting with .
Remark
Let be a topological space. Since the interval is a locally compact topological space (example ) there is the mapping space
hence the set of paths in (def. ) equipped with the compact-open topology (def. ).
This is often called the path space of .
By functoriality of the mapping space (remark ) the two endpoint inclusions
induce two continuous functions of the form
The coequalizer (example ) of these two functions is the set of path-connected components (def. ) topologized with the corresponding final topology (def. ).
Lemma
(path-connected spaces are connected)
A path connected topological space (def. ) is connected (def. ).
Proof
Assume it were not, then it would be covered by two disjoint non-empty open subsets . But by path connectedness there were a continuous path from a point in one of the open subsets to a point in the other. The continuity would imply that were a disjoint open cover of the interval. This would be in contradiction to the fact that intervals are connected. Hence we have a proof by contradiction.
Definition
(locally path-connected topological space)
A topological space is called locally path-connected if for every point and every neighbourhood there exists a neighbourhood which, as a subspace, is path-connected (def. ).
Examples
(Euclidean space is locally path-connected)
For then Euclidean space (with its metric topology) is locally path-connected, since each open ball is a path-connected topological space (example ).
Example
(open subspace of locally path-connected space is locally path-connected)
Every open subspace of a locally path-connected topological space is itself locally path-connected.
Another class of examples we consider below: locally Euclidean topological spaces are locally path-connected (prop. below).
Proposition
Let be a locally path-connected topological space (def. ). Then each of its path-connected components is an open set and a closed set.
Proof
To see that every path connected component is open, it is sufficient to show that every point has an neighbourhood which is still contained in . But by local path connectedness, has a neighbourhood which is path connected. It follows by concatenation of paths (as in the proof of lemma ) that .
Now each path-connected component is the complement of the union of all the other path-connected components. Since these are all open, their union is open, and hence the complement is closed.
Proposition
(in a locally path-connected space connected components coincide with path-connected components)
Let be a locally path-connected topological space (def. ). Then the connected components of according to def. agree with the path-connected components according to def. .
In particular, locally path connected spaces are locally connected topological spaces (def. ).
Proof
A path connected component is always connected by lemma , and in a locally path-connected space it is also open, by prop. . This implies that the path-connected components are maximal connected subspaces, and hence must be the connected components.
Conversely let be a connected component. It is now sufficient to see that this is path-connected. Suppose it were not, then it would be covered by more than one disjoint non-empty path-connected components. But by prop. these would all be open. This would be in contradiction with the assumption that is connected. Hence we have a proof by contradiction.
Embeddings
Often it is important to know whether a given space is homeomorphism to its image, under some continuous function, in some other space. This concept of embedding of topological spaces (def. below) we will later refine to that of embedding of smooth manifolds (below).
Definition
(embedding of topological spaces)
Let and be topological spaces. A continuous function is called an embedding of topological spaces if in its image factorization (example )
with the image equipped with the subspace topology (example ), we have that is a homeomorphism (def. ).
Proposition
(open/closed continuous injections are embeddings)
A continuous function which is
-
an open map or a closed map (def. )
is an embedding of topological spaces (def. ).
This is called a closed embedding if the image is a closed subset.
Proof
If is injective, then the map onto its image is a bijection. Moreover, it is still continuous with respect to the subspace topology on (example ). Now a bijective continuous function is a homeomorphism precisely if it is an open map or a closed map, by prop. . But the image projection of has this property, respectively, if does, by prop .
The following characterization of closed embeddings uses concepts of (locally) compact spaces discussed below. The reader may wish to skip the following and only compact back to it in the discussion of embeddings of smooth manifolds further bellow in prop. .
Proposition
(injective proper maps to locally compact spaces are equivalently the closed embeddings)
Let
-
be a topological space,
-
a locally compact topological space (def. ),
Then the following are equivalent:
-
is an injective proper map (prop. ),
-
is a closed embedding of topological spaces (def ).
Proof
In one direction, if is an injective proper map, then since proper maps to locally compact spaces are closed (prop. ), we have that is also closed map. The claim then follows since closed injections are embeddings (prop. ), and since the image of a closed map is closed, by definition.
Conversely, if is a closed embedding, we only need to show that the embedding map is proper. So for a compact subspace, we need to show that the pre-image is also compact. But since is an injection (being an embedding), that pre-image is equivalently just the intersection , regarded as a subspace of .
To see that this is compact, let be an open cover of the subspace , hence, by the nature of the subspace topology, let be a set of open subsets of , which cover and with the restriction of to . Now since is closed by assumption, it follows that the complement is open and hence that
is an open cover of . By compactness of this has a finite subcover. Since restricting that finite subcover back to makes the potential element disappear, this restriction is a finite subcover of . This shows that is compact.
Compact spaces
We discuss compact topological spaces (def below), the generalization of compact metric spaces above. Compact spaces are in some sense the “small” objects among topological spaces, analogous in topology to what finite sets are in set theory, or what finite-dimensional vector spaces are in linear algebra, and equally important in the theory.
Prop. suggests the following simple definition :
Definition
An open cover of a topological space (def. ) is a set of open subsets of , indexed by some set , such that their union is all of : .
A subcover of a cover is a subset such that is still a cover.
Definition
A topological space (def. ) is called a compact topological space if every open cover (def. ) has a finite subcover in that there is a finite subset such that is still a cover of in that also .
Remark
(varying terminology regarding “compact”)
Beware the following terminology issue which persists in the literature:
Some authors use “compact” to mean “Hausdorff and compact”. To disambiguate this, some authors (mostly in algebraic geometry, but also for instance Waldhausen) say “quasi-compact” for what we call “compact” in def. .
There are several equivalent reformulations of the compactness condition. An immediate reformulation is prop. , a more subtle one is prop. further below.
Proposition
(compactness in terms of closed subsets)
Let be a topological space. Then the following are equivalent:
-
is compact in the sense of def. .
-
Let be a set of closed subsets (def. ) such that their intersection is empty , then there is a finite subset such that the corresponding finite intersection is still empty .
-
Let be a set of closed subsets (def. ) such that it enjoys the finite intersection property, meaning that for every finite subset then the corresponding finite intersection is non-empty . Then also the total intersection is non-empty, .
Proof
The equivalence between the first and the second statement is immediate from the definitions after expressing open subsets as complements of closed subsets and applying de Morgan's law (prop. ).
We discuss the equivalence between the first and the third statement:
In one direction, assume that is compact in the sense of def. , and that satisfies the finite intersection property. We need to show that then .
Assume that this were not the case, hence assume that . This would imply that the open complements were an open cover of (def. )
because (using de Morgan's law, prop. )
But then by compactness of there were a finite subset such that were still an open cover, hence that . Translating this back through the de Morgan's law again this would mean that
This would be in contradiction with the finite intersection property of , and hence we have proof by contradiction.
Conversely, assume that every set of closed subsets in with the finite intersection property has non-empty total intersection. We need to show that the every open cover of has a finite subcover.
Write for the closed complements of these open subsets.
Assume on the contrary that there were no finite subset such that , hence no finite subset such that . This would mean that satisfied the finite intersection property.
But by assumption this would imply that , which, again by de Morgan, would mean that . But this contradicts the assumption that the are a cover. Hence we have a proof by contradiction.
Example
(finite discrete spaces are compact)
A discrete topological space (def. ) is compact (def. ) precisely if its underlying set is a finite set.
Example
(closed intervals are compact topological spaces)
For any the closed interval (example )
regarded with its subspace topology of Euclidean space (example ) with its metric topology (example ) is a compact topological space (def. ).
Proof
Since all the closed intervals are homeomorphic (by example ) it is sufficient to show the statement for . Hence let be an open cover (def. ). We need to show that it has an open subcover.
Say that an element is admissible if the closed sub-interval is covered by finitely many of the . In this terminology, what we need to show is that is admissible.
Observe from the definition that
-
0 is admissible,
-
if and is admissible, then also is admissible.
This means that the set of admissible forms either
-
or a closed interval ,
for some . We need to show that the latter is true, and for . We do so by observing that the alternatives lead to contradictions:
-
Assume that the set of admissible values were an open interval . Pick an such that (this exists because of the covering property). Since such is an open neighbourhood of , there is a positive real number such that the open ball is still contained in the patch. It follows that there is an element and such that there is a finite subset with a finite open cover of . It follows that were a finite open cover of , hence that itself were still admissible, in contradiction to the assumption.
-
Assume that the set of admissible values were a closed interval for . By assumption there would then be a finite set such that were a finite cover of . Hence there would be an index such that . But then by the nature of open subsets in the Euclidean space , this would also contain an open ball . This would mean that the set of admissible values includes the open interval , contradicting the assumption.
This gives a proof by contradiction.
In contrast:
Nonexample
(Euclidean space is non-compact)
For all , , the Euclidean space (example ), regarded with its metric topology (example ), is not a compact topological space (def. ).
Proof
Pick any . Consider the open cover of given by
This is not a finite cover, and removing any one of its patches , it ceases to be a cover, since the points of the form are contained only in and in no other patch.
Below we prove the Heine-Borel theorem (prop. ) which generalizes example and example .
Example
(unions and intersection9] of [[compact spaces?)
Let be a topological space and let
be a set of compact subspaces.
-
If is a finite set, then the union is itself a compact subspace;
-
If all are also closed subsets then their intersection is itself a compact subspace.
Example
(complement of compact by open subspaces is compact)
Let be a topological space. Let
-
be an open subset.
Then the complement
is itself a compact subspace.
In analysis, the extreme value theorem (example below) asserts that a real-valued continuous function on the bounded closed interval (def. ) attains its maximum and minimum. The following is the generalization of this statement to general topological spaces, cast in terms of the more abstract concept of compactness from def. :
Lemma
(continuous surjections out of compact spaces have compact codomain)
Let be a continuous function between topological spaces such that
-
is a compact topological space (def. );
-
is a surjective function.
Then also is compact.
Proof
Let be an open cover of (def. ). We need show that this has a finite sub-cover.
By the continuity of the pre-images form an open cover of . Hence by compactness of , there exists a finite subset such that is still an open cover of . Finally, by surjectivity of it it follows that
where we used that images of unions are unions of images.
This means that also is still an open cover of , and in particular a finite subcover of the original cover.
As a direct corollary of lemma we obtain:
Proposition
(continuous images of compact spaces are compact)
If is a continuous function out of a compact topological space (def. ) which is not necessarily surjective, then we may consider its image factorization
as in example . Now by construction is surjective, and so lemma implies that is compact.
The converse to cor. does not hold in general: the pre-image of a compact subset under a continuous function need not be compact again. If this is the case, then we speak of proper maps:
Definition
A continuous function is called proper if for a compact topological subspace of , then also its pre-image is compact in .
As a first useful application of the topological concept of compactness we obtain a quick proof of the following classical result from analysis:
Proposition
Let be a compact topological space (def. ), and let
be a continuous function to the real numbers equipped with their Euclidean metric topology.
Then attains its maximum and its minimum in that there exist such that
Proof
Since continuous images of compact spaces are compact (prop. ) the image is a compact subspace.
Suppose this image did not contain its maximum. Then were an open cover of the image, and hence, by its compactness, there would be a finite subcover, hence a finite set of points , such that the union of the and hence the single set alone would cover the image. This were in contradiction to the assumption that and hence we have a proof by contradiction.
Similarly for the minimum.
And as a special case:
Example
(traditional extreme value theorem)
Let
be a continuous function from a bounded closed interval () (def. ) regarded as a topological subspace (example ) of real numbers to the real numbers, with the latter regarded with their Euclidean metric topology (example , example ).
Then attains its maximum and minimum: there exists such that for all we have
Proof
Since continuous images of compact spaces are compact (prop. ) the image is a compact subspace (def. , example ). By the Heine-Borel theorem (prop. ) this is a bounded closed subset (def. , def. ). By the nature of the Euclidean metric topology, the image is hence a union of closed intervals. Finally by continuity of it needs to be a single closed interval, hence (being bounded) of the form
There is also the following more powerful equivalent reformulation of compactness:
Proposition
(closed-projection characterization of compactness)
Let be a topological space. The following are equivalent:
-
is a compact topological space according to def. ;
-
For every topological space then the projection map out of the product topological space (example , example )
is a closed map.
Proof
In one direction, assume that is compact and let be a closed subset. We need to show that is closed.
By lemma this is equivalent to showing that every point in the complement of has an open neighbourhood which does not intersect :
This is clearly equivalent to
and this is what we will show.
To this end, consider the set
Observe that this is an open cover of : For every then by assumption of , and by closure of this means that there exists an open neighbourhood of in not intersecting , and by nature of the product topology this contains an open neighbourhood of the form .
Hence by compactness of , there exists a finite subcover of and a corresponding set with .
The resulting open neighbourhood
of has the required property:
Now for the converse:
Assume that is a closed map for all . We need to show that is compact. By prop. this means equivalently that for every set of closed subsets and satisfying the finite intersection property, we need to show that .
So consider such a set of closed subsets satisfying the finite intersection property. Construct a new topological space by setting
-
;
-
a sub-base for (def. ).
Then consider the topological closure of the “diagonal” in
We claim that there exists such that
This is because
by the assumption that is a closed map, and
by construction. So if were not in , then, by lemma , it would have an open neighbourhood not intersecting . But by definition of , the open neighbourhoods of are the unions of finite intersections of , and by the assumed finite intersection property all their finite intersections do still intersect .
Since thus , lemma gives again that all of its open neighbourhoods intersect the diagonal. By the nature of the product topology (example ) this means that for all and all open neighbourhoods we have that
By definition of this means equivalently that
for all open neighbourhoods .
But by closure of and using lemma , this means that
for all , hence that
as required.
This closed-projection characterization of compactness from prop. is most useful, for instance it yields direct proof of the following important facts in topology:
-
The tube lemma, prop. below,
-
The Tychonoff theorem, prop. below.
Lemma
Let
-
be a topological space,
-
a compact topological space (def. ),
-
a point,
-
an open subset in the product topology (example , example ),
such that the -fiber over is contained in :
Then there exists an open neighborhood of such that the “tube” around the fiber is still contained:
Proof
Let
be the complement of . Since this is closed, by prop. also its projection is closed.
Now
and hence by the closure of there is (by lemma ) an open neighbourhood with
This means equivalently that , hence that .
Proposition
(Tychonoff theorem – the product space of compact spaces is compact)
Let be a set of compact topological spaces (def. ). Then also their product space (example ) is compact.
We give a proof of the finitary case of the Tychonoff theorem using the closed-projection characterization of compactness from prop. . This elementary proof generalizes fairly directly to an elementary proof of the general case: see here.
Proof of the finitary case
By prop. it is sufficient to show that for every topological space then the projection
is a closed map. We proceed by induction. For the statement is obvious. Suppose it has been proven for some . Then the projection for factors is the composite of two consecutive projections
By prop. , the first map here is closed since is compact by the assumption of the proposition, and similarly the second is closed by induction assumption. Hence the composite is a closed map.
Of course we also want to claim that sequentially compact metric spaces (def. ) are compact as topological spaces when regarded with their metric topology (example ):
Definition
(converging sequence in a topological space)
Let be a topological space (def. ) and let be a sequence of points in (def. ). We say that this sequence converges in to a point , denoted
if for each open neighbourhood of there exists a such that for all then :
Accordingly it makes sense to consider the following:
Definition
(sequentially compact topological space)
Let be a topological space (def. ). It is called sequentially compact if for every sequence of points in (def. ) there exists a sub-sequence which converges according to def. .
Proposition
(sequentially compact metric spaces are equivalently compact metric spaces)
If is a metric space (def. ), regarded as a topological space via its metric topology (example ), then the following are equivalent:
-
is a compact topological space (def. ).
-
is a sequentially compact metric space (def. ) hence a sequentially compact topological space (def. ).
Proof
Assume first that is a compact topological space. Let be a sequence in . We need to show that it has a sub-sequence which converges.
Consider the topological closures of the sub-sequences that omit the first elements of the sequence
and write
for their open complements.
Assume now that the intersection of all the were empty
or equivalently that the union of all the were all of
hence that were an open cover. By the assumption that is compact, this would imply that there were a finite subset with
This in turn would mean that , which contradicts the construction of . Hence we have a proof by contradiction that assumption is wrong, and hence that there must exist an element
By definition of topological closure this means that for all the open ball around of radius must intersect the th of the above subsequences:
If we choose one point in the th such intersection for all this defines a sub-sequence, which converges to .
In summary this proves that compact implies sequentially compact for metric spaces.
For the converse, assume now that is sequentially compact. Let be an open cover of . We need to show that there exists a finite sub-cover.
Now by the Lebesgue number lemma, there exists a positive real number such that for each there is such that . Moreover, since sequentially compact metric spaces are totally bounded, there exists then a finite set such that
Therefore is a finite sub-cover as required.
Remark
(neither compactness nor sequential compactness implies the other)
Beware, in contrast to prop. , general topological spaces being sequentially compact neither implies nor is implied by being compact.
-
The product topological space (example ) of copies of the discrete topological space (example ) indexed by the elements of the half-open interval is compact by the Tychonoff theorem (prop. ), but the sequence with
has no convergent subsequence.
-
conversely, there are spaces that are sequentially compact, but not compact, see for instance Vermeeren 10, prop. 18.
Remark
(nets fix the shortcomings of sequences)
That compactness of topological spaces is not detected by convergence of sequences (remark ) may be regarded as a shortcoming of the concept of sequence. While a sequence is indexed over the natural numbers, the concept of convergence of sequences only invokes that the natural numbers form a directed set. Hence the concept of convergence immediately generalizes to sets of points in a space which are indexed over an arbitrary directed set. This is called a net.
And with these the expected statement does become true (for a proof see here):
A topological space is compact precisely if every net in has a converging subnet.
In fact convergence of nets also detects closed subsets in topological spaces (hence their topology as such), and it detects the continuity of functions between topological spaces. It also detects for instance the Hausdorff property. (For detailed statements and proofs see here.) Hence when analysis is cast in terms of nets instead of just sequences, then it raises to the same level of generality as topology.
Compact Hausdorff spaces
We discuss some important relations between the concepts of compact topological spaces (def. ) and of Hausdorff topological spaces (def. ).
Proposition
(closed subspaces of compact Hausdorff spaces are equivalently compact subspaces)
Let
-
be a compact Hausdorff topological space (def. , def. )
-
be a topological subspace (example ).
Then the following are equivalent:
-
is a closed subspace (def. );
-
is a compact topological space (def. ).
Lemma
(closed subspaces of compact spaces are compact)
Let
-
be a compact topological space (def. ),
-
be a closed topological subspace (def. , example ).
Then also is compact.
Proof
Let be an open cover of (def. ). We need to show that this has a finite sub-cover.
By definition of the subspace topology, there exist open subsets with
By the assumption that is closed, the complement is an open subset of , and therefore
is an open cover of (def. ). Now by the assumption that is compact, this latter cover has a finite subcover, hence there exists a finite subset such that
is still an open cover of , hence in particular restricts to a finite open cover of . But since , it follows that
is a cover of , and in indeed a finite subcover of the original one.
Lemma
(compact subspaces in Hausdorff spaces are separated by neighbourhoods from points)
Let
-
be a Hausdorff topological space (def. );
Then for every there exists
-
an open neighbourhood ;
-
an open neighbourhood
such that
- they are still disjoint: .
Proof
By the assumption that is Hausdorff, we find for every point disjoint open neighbourhoods and . By the nature of the subspace topology of , the restriction of all the to is an open cover of :
Now by the assumption that is compact, there exists a finite subcover, hence a finite set such that
is still a cover.
But the finite intersection
of the corresponding open neighbourhoods of is still open, and by construction it is disjoint from all the , hence also from their union
Therefore and are two open subsets as required.
Lemma immediately implies the following:
Lemma
(compact subspaces of Hausdorff spaces are closed)
Let
-
be a Hausdorff topological space (def. )
-
be a compact (def. ) topological subspace (example ).
Then is also a closed subspace (def. ).
Proof
Let be any point of not contained in . By lemma we need to show that there exists an open neighbourhood of in which does not intersect . This is implied by lemma .
Proposition
For , consider as the -dimensional Euclidean space via example , regarded as a topological space via its metric topology (example ).
Then for a topological subspace the following are equivalent:
Proof
First consider a subset which is closed and bounded. We need to show that regarded as a topological subspace it is compact.
The assumption that is bounded by (hence contained in) some open ball in implies that it is contained in . By example , this topological subspace is homeomorphic to the -cube
hence to the product topological space (example ) of copies of the closed interval with itself.
Since the closed interval is compact by example , the Tychonoff theorem (prop. ) implies that this -cube is compact.
Since subsets are closed in a closed subspace precisely if they are closed in the ambient space (lemma ) the closed subset is also closed as a subset . Since closed subspaces of compact spaces are compact (lemma ) this implies that is compact.
Conversely, assume that is a compact subspace. We need to show that it is closed and bounded.
The first statement follows since the Euclidean space is Hausdorff (example ) and since compact subspaces of Hausdorff spaces are closed (prop. ).
Hence what remains is to show that is bounded.
To that end, choose any positive real number and consider the open cover of all of by the open n-cubes
for n-tuples of integers . The restrictions of these to hence form an open cover of the subspace . By the assumption that is compact, there is then a finite subset of -tuples of integers such that the corresponding -cubes still cover . But the union of any finite number of bounded closed -cubes in is clearly a bounded subset, and hence so is .
For the record, we list some examples of compact Hausdorff spaces that are immediately identified by the Heine-Borel theorem (prop. ):
Example
(examples of compact Hausdorff spaces)
We list some basic examples of compact Hausdorff spaces (def. , def. )
- For , the n-sphere may canonically be regarded as a topological subspace of Euclidean space (example ).
These are clearly closed and bounded subspaces of Euclidean space, hence they are compact topological space, by the Heine-Borel theorem, prop. .
Proposition
(maps from compact spaces to Hausdorff spaces are closed and proper)
Let be a continuous function between topological spaces such that
-
is a compact topological space (def. );
-
is a Hausdorff topological space (def. ).
Then is
-
a closed map (def. );
-
a proper map (def. ).
Proof
For the first statement, we need to show that if is a closed subset of , then also is a closed subset of .
Now
-
since closed subspaces of compact spaces are compact (lemma ) it follows that is also compact;
-
since continuous images of compact spaces are compact (cor. ) it then follows that is compact;
-
since compact subspaces of Hausdorff spaces are closed (prop. ) it finally follow that is also closed in .
For the second statement we need to show that if is a compact subset, then also its pre-image is compact.
Now
-
since compact subspaces of Hausdorff spaces are closed (prop. ) it follows that is closed;
-
since pre-images under continuous functions of closed subsets are closed (prop. ), also is closed;
-
since closed subspaces of compact spaces are compact (lemma ), it follows that is compact.
As an immediate corollary we record this useful statement:
Proposition
(continuous bijections from compact spaces to Hausdorff spaces are homeomorphisms)
Let be a continuous function between topological spaces such that
-
is a compact topological space (def. );
-
is a Hausdorff topological space (def. ).
Then is a homeomorphism (def. )
In particular then both and are compact Hausdorff spaces.
Proof
By prop. it is sufficient to show that is a closed map. This is the case by prop. .
Proposition
(compact Hausdorff spaces are normal)
Every compact Hausdorff topological space (def. , def. ) is a normal topological space (def. ).
Proof
First we claim that is regular. To show this, we need to find for each point and each closed subset not containing disjoint open neighbourhoods and . But since closed subspaces of compact spaces are compact (lemma ), the subset is in fact compact, and hence this is the statement of lemma .
Next to show that is indeed normal, we apply the idea of the proof of lemma once more:
Let be two disjoint closed subspaces. By the previous statement then for every point we find disjoint open neighbourhoods and . The union of the is a cover of , and by compactness of there is a finite subset such that
is an open neighbourhood of and
is an open neighbourhood of , and both are disjoint.
We discuss some important relations between the concept of compact topological spaces and that of quotient topological spaces.
Proposition
(continuous surjections from compact spaces to Hausdorff spaces are quotient projections)
Let
be a continuous function between topological spaces such that
-
is a compact topological space (def. );
-
is a Hausdorff topological space (def. );
-
is a surjective function.
Then is the quotient topology inherited from via the surjection (def. ).
Proof
We need to show that a subset is an open subset of precisely if its pre-image is an open subset in . Equivalently, as in prop. , we need to show that is a closed subset precisely if is a closed subset. The implication
follows via prop. from the continuity of . The implication
follows since is a closed map by prop. .
The following proposition allows to recognize when a quotient space of a compact Hausdorff space is itself still Hausdorff.
Proposition
Let
be a continuous function between topological spaces such that
-
is a compact Hausdorff topological space (def. , def. );
-
is a surjection and is the corresponding quotient topology (def. ).
Then the following are equivalent
-
is itself a Hausdorff topological space (def. );
-
is a closed map (def. ).
Proof
The implication is given by prop. . We need to show the converse.
Hence assume that is a closed map. We need to show that for every pair of distinct points there exist open neighbourhoods which are disjoint, .
First notice that the singleton subsets are closed. This is because they are images of singleton subsets in , by surjectivity of , and because singletons in a Hausdorff space are closed by prop, and prop. , and because images under of closed subsets are closed, by the assumption that is a closed map.
It follows that the pre-images
are closed subsets of .
Now again since compact Hausdorff spaces are normal (prop. ) it follows (by def. ) that we may find disjoint open subset such that
Moreover, by lemma we may find these such that they are both saturated subsets (def. ). Therefore finally lemma says that the images are open in . These are now clearly disjoint open neighbourhoods of and .
Example
Consider the function
-
from the quotient topological space (def. ) of the closed interval (def. ) by the equivalence relation which identifies the two endpoints
-
to the unit circle (def. ) regarded as a topological subspace of the 2-dimensional Euclidean space (example ) equipped with its
metric topology (example ).
This is clearly a continuous function and a bijection on the underlying sets. Moreover, since continuous images of compact spaces are compact (cor. ) and since the closed interval is compact (example ) we also obtain another proof that the circle is compact.
Hence by prop. the above map is in fact a homeomorphism
Compare this to the counter-example , which observed that the analogous function
is not a homeomorphism, even though this, too, is a bijection on the the underlying sets. But the half-open interval is not compact (for instance by the Heine-Borel theorem, prop. ), and hence prop. does not apply.
Locally compact spaces
A topological space is locally compact if each point has a compact neighbourhood. Or rather, this is the case in locally compact Hausdorff spaces. Without the Hausdorff condition one asks that these compact neighbourhoods exist in a certain controlled way (def. below).
It turns out (prop. below) that locally compact Hausdorff spaces are precisely the open subspaces of the compact Hausdorff spaces discussed above.
A key application of local compactness is that the mapping spaces (topological spaces of continuous functions, def. below) out of a locally compact space behave as expected from mapping spaces. (prop. below). This gives rise for instance the loop spaces and path spaces (example below) which become of paramount importance in the discussion of homotopy theory.
For the purposes of point-set topology local compactness is useful as a criterion for identifying paracompactness (prop. below).
Definition
(locally compact topological space)
A topological space is called locally compact if for every point and every open neighbourhood there exists a smaller open neighbourhood whose topological closure is compact (def. ) and still contained in :
Remark
(varying terminology regarding “locally compact”)
On top of the terminology issue inherited from that of “compact”, remark (regarding whether or not to require “Hausdorff” with “compact”; we do not), the definition of “locally compact” is subject to further ambiguity in the literature. There are various definitions of locally compact spaces alternative to def. , we consider one such alternative definition below in def. .
For Hausdorff topological spaces all these definitions happen to be equivalent (prop. below), but in general they are not.
Example
(discrete spaces are locally compact)
Every discrete topological space (example ) is locally compact (def. ).
Example
(Euclidean space is locally compact)
For then Euclidean space (example ) regarded as a topological space via its metric topology (def. ), is locally compact (def. ).
Proof
Let be a point and an open neighbourhood. By definition of the metric topology (example ) this means that contains an open ball (def. ) around of some radius . This ball also contains the open ball and its topological closure, which is the closed ball . This closed ball is compact, for instance by the Heine-Borel theorem (prop. ).
Example
(open subspaces of compact Hausdorff spaces are locally compact)
Every open topological subspace of a compact (def. ) Hausdorff space (def. ) is a locally compact topological space (def. ).
In particular compact Hausdorff spaces themselves are locally compact.
Proof
Let be a topological space such that it arises as a topological subspace of a compact Hausdorff space. We need to show that is a locally compact topological space (def. ).
Let be a point and let an open neighbourhood. We need to produce a smaller open neighbourhood whose closure is compact and still contained in .
By the nature of the subspace topology there exists an open subset such that . Since is assumed to be open, it follows that is also open as a subset of . Since compact Hausdorff spaces are normal (prop. ) it follows by prop. that there exists a smaller open neighbourhood whose topological closure is still contained in , and since closed subspaces of compact spaces are compact (prop. ), this topological closure is compact:
The intersection of this situation with is the required smaller compact neighbourhood :
Example
(finite product space of locally compact spaces is locally compact)
The product topological space (example ) of a a finite set of locally compact topological spaces (def. ) it itself locally compact.
Nonexample
(countably infinite products of non-compact spaces are not locally compact)
Let be a topological space which is not compact (def. ). Then the product topological space (example ) of a countably infinite set of copies of
is not a locally compact space (def. ).
Proof
Since the continuous image of a compact space is compact (prop. ), and since the projection maps are continuous (by nature of the initial topology/Tychonoff topology), it follows that every compact subspace of the product space is contained in one of the form
for compact.
But by the nature of the Tychonoff topology, a base for the topology on is given by subsets of the form
with open. Hence every compact neighbourhood in contains a subset of this kind, but if itself is non-compact, then none of these is contained in a product of compact subsets.
In the discussion of locally Euclidean spaces (def. below), as well as in other contexts, a definition of local compactness that in the absence of Hausdorffness is slightly weaker than def. (recall remark ) is useful:
Definition
(local compactness via compact neighbourhood base)
A topological space is locally compact if for for every point every open neighbourhood contains a compact neighbourhood .
Proposition
(equivalence of definitions of local compactness for Hausdorff spaces)
If is a Hausdorff topological space, then the two definitions of local compactness of
-
definition (every open neighbourhood contains a compact neighbourhood),
-
definition (every open neighbourhood contains a compact neighbourhood that is the topological closure of an open neighbourhood)
are equivalent.
Proof
Generally, definition directly implies definition . We need to show that Hausdorffness implies the converse.
Hence assume that for every point then every open neighbourhood contains a compact neighbourhood. We need to show that it then also contains the closure of a smaller open neighbourhood and such that this closure is compact.
So let be a compact neighbourhood. Being a neighbourhood, it has a non-trivial interior which is an open neighbourhood
Since compact subspaces of Hausdorff spaces are closed (lemma ), it follows that is a closed subset. This implies that the topological closure of its interior as a subset of is still contained in (since the topological closure is the smallest closed subset containing the given subset, by def. ): . Since subsets are closed in a closed subspace precisely if they are closed in the ambient space (lemma ), is also closed as a subset of the compact subspace . Now since closed subspaces of compact spaces are compact (lemma ), it follows that this closure is also compact as a subspace of , and since continuous images of compact spaces are compact (prop. ), it finally follows that it is also compact as a subspace of :
A key application of locally compact spaces is that the space of maps out of them into any given topological space (example below) satisfies the expected universal property of a mapping space (prop. below).
Example
(topological mapping space with compact-open topology)
For
-
a locally compact topological space (in the sense of def. or just in the sense of def. )
then the mapping space
is the topological space
-
whose underlying set is the set of continuous functions ;
-
whose topology is generated from the sub-basis for the topology (def. ) which is given by subsets to denoted
for labels
-
a compact subset,
-
an open subset
and defined to be those subsets of all those continuous functions that take to :
-
Accordingly this topology is called the compact-open topology on the set of functions.
Proposition
(universal property of the mapping space)
Let , , be topological spaces, with locally compact (def. or just def. ). Then
-
The evaluation function
is a continuous function.
-
The natural bijection of function sets
restricts to a natural bijection between sets of continuous functions
Here is the mapping space with compact-open topology from example and denotes forming the product topological space (example , example ).
Proof
To see the continuity of the evaluation map:
Let be an open subset. It is sufficient to show that is a union of products of the form with open and a basic open according to def. .
For , the preimage is an open neighbourhood of in , by continuity of .
By local compactness of , there is a compact subset which is still a neighbourhood of , hence contains an open neighbourhood . Since also still takes that into , we have found an open neighbourhood
with respect to the product topology. Since this is still contained in , for all as above, is exhibited as a union of opens, and is hence itself open.
Regarding the second point:
In one direction, let be a continuous function, and let be a sub-basic open. We need to show that the set
is open. To that end, observe that means that , where is open by the continuity of . Hence in the topological subspace the inclusion
is an open neighbourhood. Since is compact, the tube lemma (prop. ) gives an open neighbourhood in , hence an open neighbourhood , which is still contained in the original pre-image:
This shows that with every point also an open neighbourhood of is contained in , hence that the latter is a union of open subsets, and hence itself open.
In the other direction, assume that is continuous: We need to show that is continuous. But observe that is the composite
Here the first function is continuous since is by assumption since the product of two continuous functions is again continuous (example ). The second function is continuous by the first point above. hence is continuous.
Remark
(topological mapping space is exponential object)
In the language of category theory (remark ), prop. says that the mapping space construction with its compact-open topology from def. is an exponential object or internal hom. This just means that it behaves in all abstract ways just as a function set does for plain functions, but it does so for continuous functions and being itself equipped with a topology.
Moreover, the construction of topological mapping spaces in example extends to a functor (remark )
from the product category of the category Top of all topological spaces (remark ) with the opposite category of the subcategory of locally compact topological spaces.
Example
(topological mapping space construction out of the point space is the identity)
The point space (example ) is clearly a locally compact topological space. Hence for every topological space the mapping space (example ) exists. This is homeomorphic (def. ) to the space itself:
Example
(loop space and path space)
Let be any topological space.
-
The circle (example ) is a compact Hausdorff space (example ) hence, by prop. , a locally compact topological space (def. ). Accordingly the mapping space
exists (def. ). This is called the free loop space of .
If both and are equipped with a choice of point (“basepoint”) , , then the topological subspace
on those functions which take the basepoint of to that of , is called the loop space of , or sometimes based loop space, for emphasis.
-
Similarly the closed interval is a compact Hausdorff space (example ) hence, by prop. , a locally compact topological space (def. ). Accordingly the mapping space
exists (def. ). Again if is equipped with a choice of basepoint , then the topological subspace of those functions that take to that chosen basepoint is called the path space of :
Notice that we may encode these subspaces more abstractly in terms of universal properties:
The path space and the loop space are characterized, up to homeomorphisms, as being the limiting cones in the following pullback diagrams of topological spaces (example ):
Here on the right we are using that the mapping space construction is a functor as shown in remark , and we are using example in the identification on the bottom right mapping space out of the point space.
Above we have seen that open subspace of compact Hausdorff spaces are locally compact Hausdorff spaces. Now we prepare to show the converse, namely that every locally compact Hausdorff spaces arises as an open subspace of a compact Hausdorff space. That compact Hausdorff space is its “one-point compactification”:
Definition
Let be any topological space. Its one-point compactification is the topological space
-
whose underlying set is the disjoint union
-
and whose open sets are
-
the open subsets of (thought of as subsets of );
-
the complements of the closed compact subsets .
-
Remark
If is Hausdorff, then it is sufficient to speak of compact subsets in def. , since compact subspaces of Hausdorff spaces are closed.
Lemma
(one-point compactification is well-defined)
The topology on the one-point compactification in def. is indeed well defined in that the given set of subsets is indeed closed under arbitrary unions and finite intersections.
Proof
The unions and finite intersections of the open subsets inherited from are closed among themselves by the assumption that is a topological space.
It is hence sufficient to see that
-
the unions and finite intersection of the are closed among themselves,
-
the union and intersection of a subset of the form with one of the form is again of one of the two kinds.
Regarding the first statement: Under de Morgan duality
and
and so the first statement follows from the fact that finite unions of compact subspaces and arbitrary intersections of closed compact subspaces are themselves again compact (example ).
Regarding the second statement: That is open means that there exists a closed subset with . Now using de Morgan duality we find
-
for intersections:
Since finite unions of closed subsets are closed, this is again an open subset of ;
-
for unions:
For this to be open in we need that is again compact. This follows because subsets are closed in a closed subspace precisely if they are closed in the ambient space and because closed subsets of compact spaces are compact.
Example
(one-point compactification of Euclidean space is the n-sphere )
For the n-sphere with its standard topology (e.g. as a subspace of the Euclidean space with its metric topology) is homeomorphic to the one-point compactification (def. ) of the Euclidean space
Proof
Pick a point . By stereographic projection we have a homeomorphism
With this it only remains to see that for an open neighbourhood of in then the complement is compact closed, and cnversely that the complement of every compact closed subset of is an open neighbourhood of .
Observe that under stereographic projection (example ) the open subspaces are identified precisely with the closed and bounded subsets of . (Closure is immediate, boundedness follows because an open neighbourhood of needs to contain an open ball around in the other stereographic projection, which under change of chart gives a bounded subset. )
By the Heine-Borel theorem (prop. ) the closed and bounded subsets of are precisely the compact, and hence the compact closed, subsets of .
The following are the basic properties of the one-point compactification in def. :
Proposition
(one-point compactification is compact)
For any topological space, then its one-point compactification (def. ) is a compact topological space.
Proof
Let be an open cover. We need to show that this has a finite subcover.
That we have a cover means that
-
there must exist such that is an open neighbourhood of the extra point. But since, by construction, the only open subsets containing that point are of the form , it follows that there is a compact closed subset with .
-
is in particular an open cover of that closed compact subset . This being compact means that there is a finite subset so that is still a cover of .
Together this implies that
is a finite subcover of the original cover.
Proposition
(one-point compactification of locally compact space is Hausdorff precisely if original space is)
Let be a locally compact topological space. Then its one-point compactification (def. ) is a Hausdorff topological space precisely if is.
Proof
It is clear that if is not Hausdorff then is not.
For the converse, assume that is Hausdorff.
Since as underlying sets, we only need to check that for any point, then there is an open neighbourhood and an open neighbourhood of the extra point which are disjoint.
That is locally compact implies by definition that there exists an open neighbourhood whose topological closure is a closed compact neighbourhood . Hence
is an open neighbourhood of and the two are disjoint
by construction.
Proposition
(inclusion into one-point compactification is open embedding)
Let be a topological space. Then the evident inclusion function
into its one-point compactification (def. ) is
Proof
Regarding the first point: For open and closed and compact, the pre-images of the corresponding open subsets in are
which are open in .
Regarding the second point: The image of an open subset is , which is open by definition
Regarding the third point: We need to show that is a homeomorphism. This is immediate from the definition of .
As a corollary we finally obtain:
Proposition
(locally compact Hausdorff spaces are the open subspaces of compact Hausdorff spaces)
The locally compact Hausdorff spaces are, up to homeomorphism precisely the ope subspaces of compact Hausdorff spaces.
Proof
That every open subspace of a compact Hausdorff space is locally compact Hausdorff was the statement of example . It remains to see that every locally compact Hausdorff space arises this way.
But if is locally compact Hausdorff, then its one-point compactification is compact Hausdorff by prop. and prop. . Moreover the canonical embedding exhibits as an open subspace of by prop. .
We close with two observations on proper maps into locally compact spaces, which will be useful in the discussion of embeddings of smooth manifolds below.
Proposition
(proper maps to locally compact spaces are closed)
Let
-
be a topological space,
-
a locally compact Hausdorff space (def. , def. ),
-
a proper map (def. ).
Then is a closed map (def. ).
Proof
Let be a closed subset. We need to show that is closed. By lemma this means we need to show that every has an open neighbourhood not intersecting ..
By local compactness of (def. ), has an open neighbourhood whose topological closure is compact. Hence since is proper, also is compact. Then also the intersection is compact, and since continuous images of compact spaces are compact (prop. ) so is
This is also a closed subset, since compact subspaces of Hausdorff spaces are closed (lemma ). Therefore
is an open neighbourhood of not intersecting .
Proposition
(injective proper maps to locally compact spaces are equivalently the closed embeddings)
Let
-
be a topological space
-
a locally compact Hausdorff space (def. , def. ),
-
be a continuous function.
Then the following are equivalent
-
is an injective proper map,
-
is a closed embedding of topological spaces (def. ).
Proof
In one direction, if is an injective proper map, then since proper maps to locally compact spaces are closed, it follows that is also closed map. The claim then follows since closed injections are embeddings (prop. ), and since the image of a closed map is closed.
Conversely, if is a closed embedding, we only need to show that the embedding map is proper. So for a compact subspace, we need to show that the pre-image is also compact. But since is an injection (being an embedding), that pre-image is just the intersection . By the nature of the subspace topology, this is compact if is.
Paracompact spaces
The concept of compactness in topology (above) has several evident weakenings of interest. One is that of paracompactness (def. below). The concept of paracompact topological spaces leads over from plain topology to actual geometry. In particular the topological manifolds discussed below are paracompact topological spaces.
A key property is that paracompact Hausdorff spaces are equivalently those (prop. below) all whose open covers admit a subordinate partition of unity (def. below), namely a set of real-valued continuous functions each of which is supported in only one patch of the cover, but whose sum is the unit function. Existence of such partitions implies that structures on topological spaces which are glued together via linear maps (such as vector bundles) are well behaved.
Finally in algebraic topology paracompact spaces are important as for them abelian sheaf cohomology may be computed in terms of Cech cohomology.
Definition
Let be a topological space.
An open cover (def. ) of is called locally finite if for all points , there exists a neighbourhood such that it intersects only finitely many elements of the cover, hence such that for only a finite number of .
Definition
(refinement of open covers)
Let be a topological space, and let be a open cover (def. ).
Then a refinement of this open cover is a set of open subsets which is still an open cover in itself and such that for each there exists an with .
Definition
(paracompact topological space)
A topological space is called paracompact if every open cover of has a refinement (def. ) by a locally finite open cover (def. ).
Here are two basic classes of examples of paracompact spaces, below in Examples we consider more sophisticated ones:
Example
(compact topological spaces are paracompact)
Every compact topological space (def. ) is paracompact (def. ).
Since a finite subcover is in particular a locally finite refinement.
Example
(disjoint unions of paracompact spaces are paracompact)
Let be a set of paracompact topological spaces (def. ). Then also their disjoint union space (example )
is paracompact.
In particular, by example a non-finite disjoint union of compact topological spaces is, while no longer compact, still paracompact.
Proof
Let be an open cover. We need to produce a locally finite refinement.
Since each is open in the disjoint union, the intersections are all open, and hence by forming all these intersections we obtain a refinement of the original cover by a disjoint union of open covers of for all . By the assumption that each is paracompact, each has a locally finite refinement . Accordingly the disjoint union is a locally finite refinement of .
In identifying paracompact Hausdorff spaces using the recognition principles that we establish below it is often useful (as witnessed for instance by prop. and prop. below) to consider two closely related properties of topological spaces:
-
second-countability (def. below);
-
sigma-compactness (def. below)
Definition
(second-countable topological space)
A topological space is called second countable if it admits a base for its topology (def. ) which is a countable set of open subsets.
Example
(Euclidean space is second-countable)
Let . Consider the Euclidean space with its Euclidean metric topology (example , example ). Then is second countable (def. ).
A countable set of base open subsets is given by the open balls of rational radius and centered at points with rational coordinates: .
Proof
To see that this is still a base, it is sufficient to see that every point inside very open ball in is contains in an open ball of rational radius with rational coordinates of its center that is still itself contained in the original open ball.
To that end, let be a point inside an open ball and let be its distance from the boundary of the ball. By the fact that the rational numbers are a dense subset of , we may find such that and then we may find such that . This open ball contains and is contained in the original open ball.
To see that this base is countable, use that
-
the set of rational numbers is countable;
-
the Cartesian product of two countable sets is countable.
Definition
(sigma-compact topological space)
A topological space is called sigma-compact if it is the union of a countable set of compact subsets (def. ).
Example
(Euclidean space is sigma-compact)
For then the Euclidean space (example ) equipped with its metric topology (example ) is sigma-compact (def. ).
Proof
For let
be the closed ball (def. ) of radius . By the Heine-Borel theorem (prop. ) these are compact subspaces. Clearly they exhaust :
Examples
Below we consider three important classes of examples of paracompact spaces whose proof of paracompactness is non-trivial:
-
locally compacttopological groups (prop. ),
-
metric spaces (prop. ),
-
CW-complexes (example ).
In order to discuss these, we first consider some recognition principles of paracompactness:
-
locally compact and second-countable spaces are sigma-compact (prop. below)
-
locally compact and sigma-compact spaces are paracompact (prop. below)
-
second-countable regular spaces are paracompact (prop. below)
More generally, these statements are direct consequences of Michael's theorem on recognition of paracompactness (prop. below).
The first of these statements is fairly immediate:
Lemma
(locally compact and second-countable spaces are sigma-compact)
Let be a topological space which is
-
locally compact (def. ),
-
second-contable (def. ).
Then is sigma-compact (def. ).
Proof
We need to produce a countable cover of by compact subspaces.
By second-countability there exists a countable base of open subsets
By local compactness, every point has an open neighbourhood whose topological closure is compact.
By definition of base of a topology (def. ), for each there exists such that , hence such that .
Since subsets are closed in a closed subspace precisely if they are closed in the ambient space (lemma ), since is compact by assumption, and since closed subspaces of compact spaces are compact (lemma ) it follows that is compact.
Applying this for each point exhibits as a union of compact closures of base opens:
But since there is only a countable set of base open subsets to begin with, there is a countable subset such that
Hence
is a countable cover of by compact subspaces.
The other two statements need a little more preparation:
Lemma
(locally compact and sigma-compact space admits nested countable cover by coompact subspaces)
Let be a topological space which is
-
locally compact (def. );
-
sigma-compact (def. ).
Then there exists a countable open cover of such that for each
-
the topological closure (def. ) is a compact subspace (def. , example );
-
.
Proof
By sigma-compactness of there exists a countable cover of compact subspaces. We use these to construct the required cover by induction.
For set
Then assume that for we have constructed a set with the required properties.
In particular this implies that the union
is a compact subspace (by example ). We now construct an open neighbourhood of this union as follows:
Let be a set of open neighbourhood around each of the points in . By local compactness of , for each there is a smaller open neighbourhood with
So is still an open cover of . By compactness of , there exists a finite set such that is a finite open cover. The union
is an open neighbourhood of , hence in particular of . Moreover, since finite unions of compact spaces are compact (example ), and since the closure of a finite union is the union of the closures (prop. ) the closure of is compact:
In conclusion, by induction we have produced a set with compact and for all . It remains to see that this is a cover. This follows since by construction each is an open neighbourhood not just of but in fact of , hence in particular of , and since the form a cover by assumption:
Proposition
(locally compact and sigma-compact spaces are paracompact)
Let be a topological space which is
Then is also paracompact.
Proof
Let be an open cover of . We need to show that this has a refinement by a locally finite cover.
By lemma there exists a countable open cover of such that for all
-
is compact;
-
.
Notice that the complement is compact, since is compact and is open, by example .
By this compactness, the cover regarded as a cover of the subspace has a finite subcover indexed by a finite set , for each .
We consider the sets of intersections
Since is open, and since by construction, this is still an open cover of . We claim now that
is a locally finite refinement of the original cover, as required:
-
is a refinement, since by construction each element in is contained in one of the ;
-
is still a covering because by construction it covers for all , and since by the nested nature of the cover also is a cover of .
-
is locally finite because each point has an open neighbourhood of the form (since these also form an open cover, by the nestedness) and since by construction this has trivial intersection with and since all are finite, so that also is finite.
Using this, we may finally demonstrate a fundamental example of a paracompact space:
Example
(Euclidean space is paracompact)
For , the Euclidean space (example ), regarded with its metric topology (example ) is a paracompact topological space (def. ).
Proof
The Euclidean space is locally compact by example and sigma-compact by example . Therefore the statement follows since locally compact and sigma-compact spaces are paracompact (prop. ).
More generally all metric spaces are paracompact. This we consider below as prop. .
Using this recognition principle prop. , a source of paracompact spaces are locally compact topological groups (def. ), by prop. below:
Definition
A topological group is a group equipped with a topology (def. ) such that the group operation and the assignment of inverse elements are continuous functions.
Example
(Euclidean space as a topological groups)
For then the Euclidean space with its metric topology and equipped with the addition operation from its canonical vector space structure is a topological group (def. ) .
The following prop. is a useful recognition principle for paracompact topological groups:
Lemma
(open subgroups of topological groups are closed)
Every open subgroup of a topological group (def. ) is closed.
Proof
The set of -cosets is a cover of by disjoint open subsets. One of these cosets is itself and hence it is the complement of the union of the other cosets, hence the complement of an open subspace, hence closed.
Proposition
(locally compact topological groups are paracompact)
A topological group (def. ) which is locally compact (def. ) is paracompact (def. ).
Proof
By assumption of local compactness, there exists a compact neighbourhood of the neutral element. We may assume without restriction of generality that with any element, then also the inverse element .
For if this is not the case, then we may enlarge by including its inverse elements, and the result is still a compact neighbourhood of the neutral element: Since taking inverse elements is a continuous function, and since continuous images of compact spaces are compact, it follows that also the set of inverse elements to elements in is compact, and the union of two compact subspaces is still compact (example ).
Now for , write for the image of under the iterated group product operation .
Then
is clearly a topological subgroup of .
Observe that each is compact. This is because is compact by the Tychonoff theorem (prop. ), and since continuous images of compact spaces are compact. Thus
is a countable union of compact subspaces, making it sigma-compact. Since locally compact and sigma-compact spaces are paracompact (prop. ), this implies that is paracompact.
Observe also that the subgroup is open, because it contains with the interior of a non-empty open subset and we may hence write as a union of open subsets
Finally, as indicated in the proof of Lemma , the cosets of the open subgroup are all open and partition as a disjoint union space (example ) of these open cosets. From this we may draw the following conclusions:
-
In the particular case where is connected (def. ), there is just one such coset, namely itself. The argument above thus shows that a connected locally compact topological group is -compact and (by local compactness) also paracompact.
-
In the general case, all the cosets are homeomorphic to which we have just shown to be a paracompact group. Thus is a disjoint union space of paracompact spaces. This is again paracompact by prop. .
An archetypical example of a locally compact topological group is the general linear group:
Example
For the general linear group is the group of real matrices whose determinant is non-vanishing
with group operation given by matrix multiplication.
This becomes a topological group (def. ) by taking the topology on to be the subspace topology (def. ) as a subspace of the Euclidean space (example ) of matrices
with its metric topology (example ).
Since matrix multiplication is a polynomial function and since matrix inversion is a rational function, and since polynomials are continuous and more generally rational functions are continuous on their domain of definition (example ) and since the domain of definition for matrix inversion is precisely , the group operations on are indeed continuous functions.
There is another topology which suggests itself on the general linear group: the compact-open topology (example ). But in fact this coincides with the Euclidean topology:
Proposition
(general linear group is subspace of the mapping space)
The topology induced on the real general linear group when regarded as a topological subspace of Euclidean space with its metric topology
(as in def. ) coincides with the topology induced by regarding the general linear group as a subspace of the mapping space ,
i.e. the set of all continuous functions equipped with the compact-open topology.
Proof
On the one hand, the universal property of the mapping space (prop. ) gives that the inclusion
is a continuous function for equipped with the Euclidean metric topology, because this is the adjunct of the defining continuous action map
This implies that the Euclidean metric topology on is equal to or finer than the subspace topology coming from .
We conclude by showing that it is also equal to or coarser, together this then implies the claims.
Since we are speaking about a subspace topology, we may consider the open subsets of the ambient Euclidean space . Observe that a neighborhood base of a linear map or matrix consists of sets of the form
for .
But this is also a base element for the compact-open topology, namely
where is a singleton and is the open ball of radius around .
Proposition
(general linear group is paracompact Hausdorff)
The topological general linear group (def. ) is
Proof
Observe that
is an open subspace, since it is the pre-image under the determinant function (which is a polynomial and hence continuous, example ) of the of the open subspace :
As an open subspace of Euclidean space, is not compact, by the Heine-Borel theorem (prop. ).
As Euclidean space is Hausdorff (example ), and since every topological subspace of a Hausdorff space is again Hausdorff, so is Hausdorff.
Similarly, as Euclidean space is locally compact (example ) and since an open subspace of a locally compact space is again locally compact, it follows that is locally compact.
From this it follows that is paracompact, since locally compact topological groups are paracompact by prop. .
Now we turn to the second recognition principle for paracompactness and the examples it implies. For the time being the remainded of this section is without proof. The reader may wish to skip ahead to the discussion of Partitions of unity.
Proposition
Let be a topological space such that
-
is regular;
-
every open cover of has a refinement by a union of a countable set of locally finite sets of open subsets (the latter not necessarily covering).
Then is paracompact topological space.
Using this one shows:
Proposition
(metric spaces are paracompact)
A metric space (def. ) regarded as a topological space via its metric topology (example ) is paracompact (def. ).
Proposition
(second-countable regular spaces are paracompact)
Let be a topological space which is
-
second-countable (def. );
-
regular (def. ).
Then is paracompact topological space.
Proof
Let be an open cover. By Michael's theorem (prop. ) it is sufficient that we find a refinement by a countable cover (hence a countable union of sets consisting of single open subsets).
But second countability implies precisely that every open cover has a countable subcover:
Every open cover has a refinement by a cover consisting of base elements, and if there is only a countable set of these, then the resulting refinement necessarily contains at most this countable set of distinct open subsets.
Example
(CW-complexes are paracompact Hausdorff spaces)
Let be a paracompact Hausdorff space, let and let
be a continuous function from the -sphere (with its subspace topology inherited from Euclidean space, example ). Then also the attachment space (example ) , i.e. the pushout
is paracompact Hausdorff.
This immediately implies that all finite CW-complexes (def. ) relative to a paracompact Hausdorff space are themselves paracompact Hausdorff. In fact this is true generally: all CW-complexes are paracompact Hausdorff spaces.
Partitions of unity
A key aspect of paracompact Hausdorff spaces is that they are equivalently those spaces that admit partitions of unity. This is def. and prop. below. The existence of partitions of unity on topological spaces is what starts to give them “geometric character”. For instance the topological vector bundles discussed below behave as expected in the presence of partitions of unity.
Before we discuss partitions of unity, we consider some technical preliminaries on locally finite covers. First of all notice the following simple but useful fact:
Lemma
(every locally finite refinement induces one with the original index set)
Let be a topological space, let be an open cover (def. ), and let , be a refinement (def. ) to a locally finite cover (def. ).
By definition of refinement we may choose a function
such that
Then with
is still a refinement of to a locally finite cover.
Proof
It is clear by construction that , hence that we have a refinement. We need to show local finiteness.
Hence consider . By the assumption that is locally finite, it follows that there exists an open neighbourhood and a finite subset such that
Hence by construction
Since the image is still a finite set, this shows that is locally finite.
In the discussion of topological manifolds below, we are particularly interested in topological spaces that are both paracompact as well as Hausdorff. In fact these are even normal:
Proposition
(paracompact Hausdorff spaces are normal)
Every paracompact Hausdorff space (def. , def. ) is normal (def. ).
In particular compact Hausdorff spaces are normal.
Proof
Let be a paracompact Hausdorff space
We first show that it is regular: To that end, let be a point, and let be a closed subset not containing . We need to find disjoint open neighbourhoods and .
First of all, by the Hausdorff property there exists for each disjoint open neighbourhoods and . As ranges, the latter clearly form an open cover of , and so the union
is an open cover of . By paracompactness of , there exists a locally finite refinement, and by lemma we may assume its elements to share the original index set and be contained in the original elements of the same index. Hence
is a locally finite collection of subsets, such that
is an open neighbourhood of .
Now by definition of local finiteness there exists an open neighbourhood and a finite subset such that
Consider then
which is an open neighbourhood of , by the finiteness of .
It thus only remains to see that
But this holds because the only that intersect are the for and each of these is by construction disjoint from and hence from .
This establishes that is regular. Now we prove that it is normal. For this we use the same approach as before:
Let be two disjoint closed subsets. By need to produce disjoint open neighbourhoods for these.
By the previous statement of regularity, we may find for each disjoint open neighbourhoods and . Hence the union
is an open cover of , and thus by paracompactness has a locally finite refinement, whose elements we may, again by lemma , assume to have the same index set as before and be contained in the previous elements with the same index. Hence we obtain a locally finite collection of subsets
such that
is an open neighbourhood of .
It is now sufficient to see that every point has an open neighbourhood not intersecting , for then
is the required open neighbourhood of not intersecting .
Now by local finiteness of , every has an open neighbourhood such that there is a finite set so that
Accordingly the intersection
is still open and disjoint from the remaining , hence disjoint from all of .
That paracompact Hausdorff spaces are normal (prop. ) allows to “shrink” the open subsets of any locally finite open cover a little, such that the topological closure of the small patch is still contained in the original one:
Lemma
(shrinking lemma for locally finite covers)
Let be a topological space which is normal (def. ) and let be a locally finite open cover (def. ).
Then there exists another open cover such that the topological closure of its elements is contained in the original patches:
We now prove the shrinking lemma in increasing generality; first for binary open covers (lemma below), then for finite covers (lemma ), then for locally finite countable covers (lemma ), and finally for general locally finite covers (lemma , proof below). The last statement needs the axiom of choice.
Lemma
(shrinking lemma for binary covers)
Let be a normal topological space and let an open cover by two open subsets.
Then there exists an open set whose topological closure is contained in
and such that is still an open cover of .
Proof
Since it follows (by de Morgan's law, prop. ) that their complements are disjoint closed subsets. Hence by normality of there exist disjoint open subsets
By their disjointness, we have the following inclusions:
In particular, since is closed, this means that .
Hence it only remains to observe that , which is true by definition of .
Lemma
(shrinking lemma for finite covers)
Let be a normal topological space, and let be an open cover with a finite number of patches. Then there exists another open cover such that for all .
Proof
By induction, using lemma .
To begin with, consider . This is a binary open cover, and hence lemma gives an open subset with such that is still an open cover, and accordingly so is
Similarly we next find an open subset with and such that
is an open cover. After such steps we are left with an open cover as required.
Remark
Beware the induction in lemma does not give the statement for infinite countable covers. The issue is that it is not guaranteed that is a cover.
And in fact, assuming the axiom of choice, then there exists a counter-example of a countable cover on a normal spaces for which the shrinking lemma fails (a Dowker space due to Beslagic 85).
This issue is evaded if we consider locally finite countable covers:
Lemma
(shrinking lemma for locally finite countable covers)
Let be a normal topological space and a locally finite countable cover. Then there exists open subsets for such that and such that is still a cover.
Proof
As in the proof of lemma , there exist for such that and such that for every finite number, hence every , then
Now the extra assumption that is locally finite implies that every is contained in only finitely many of the , hence that for every there exists such that
This implies that for every then
hence that is indeed a cover of .
This is as far as one gets without the axiom of choice. We now invoke Zorn's lemma to generalize the shrinking lemma for finitely many patches (lemma ) to arbitrary sets of patches:
Proof
of the general shrinking lemma, lemma .
Let be the given locally finite cover of the normal space . Consider the set of pairs consisting of
-
a subset ;
-
an -indexed set of open subsets
with the property that
-
;
-
.
-
is an open cover of .
Equip the set with a partial order by setting
By definition, an element of with is an open cover of the required form.
We claim now that a maximal element of has .
For assume on the contrary that is maximal and there were . Then we could apply the construction in lemma to replace that single with a smaller open subset to obtain such that and such that is still an open cover. But that would mean that , contradicting the assumption that is maximal. This proves by contradiction that a maximal element of has and hence is an open cover as required.
We are reduced now to showing that a maximal element of exists. To achieve this we invoke Zorn's lemma. Hence we have to check that every chain in , hence every totally ordered subset has an upper bound.
So let be a totally ordered subset. Consider the union of all the index sets appearing in the pairs in this subset:
Now define open subsets for picking any in with and setting
This is independent of the choice of , hence well defined, by the assumption that is totally ordered.
Moreover, for define
We claim now that thus defined is a cover of . Because by assumption that is locally finite, so for every point there exists a finite set such that . Since is a total order, it must contain an element such that the finite set is contained in its index set , hence . Since that is a cover, it follows that , hence in .
This shows that is indeed an element of . It is clear by construction that it is an upper bound for . Hence we have shown that every chain in has an upper bound, and so Zorn’s lemma implies the claim.
After these preliminaries, we finally turn to the partitions of unity:
Definition
Let be a topological space, and let be an open cover. Then a partition of unity subordinate to the cover is
-
a set of continuous functions
(where is equipped with the subspace topology of the real numbers regarded as the 1-dimensional Euclidean space equipped with its metric topology);
such that with
denoting the support of (the topological closure of the subset of points on which it does not vanish) then
-
;
-
is a locally finite cover (def. );
-
.
Remark
Regarding the definition of partition of unity (def. ) observe that:
-
Due to the second clause in def. , the sum in the third clause involves only a finite number of elements not equal to zero, and therefore is well defined.
-
Due to the third clause, the interiors of the supports constitute a locally finite open cover:
-
they are open, since they are the pre-images under the continuous functions of the open subset ,
-
they cover because, by the third clause, for each there is at least one with , hence
-
they are locally finite because by the second clause already their closures are locally finite.
-
Example
Consider with its Euclidean metric topology.
Let and consider the open cover
Then a partition of unity (def. )) subordinate to this cover is given by
Proposition
(paracompact Hausdorff spaces equivalently admit subordinate partitions of unity)
Let be a Hausdorff topological space (def. ). Then the following are equivalent:
-
is a paracompact topological space (def. ).
-
Every open cover of admits a subordinate partition of unity (def. ).
Proof
One direction is immediate: Assume that every open cover admits a subordinate partition of unity . Then by definition (def. ) is a locally finite open cover refining the original one (remark ), hence is paracompact.
We need to show the converse: If is a paracompact topological space, then for every open cover there is a subordinate partition of unity (def. ).
By paracompactness of , for every open cover there exists a locally finite refinement , and by lemma we may assume that this has the same index set. It is now sufficient to show that this locally finite cover admits a subordinate partition of unity, since this will then also be subordinate to the original cover.
Since paracompact Hausdorff spaces are normal (prop. ) we may apply the shrinking lemma to the given locally finite open cover , to obtain a smaller locally finite open cover . Apply the lemma once more to that result to get a yet smaller open cover , so that now
It follows that for each we have two disjoint closed subsets, namely the topological closure and the complement
Now since paracompact Hausdorff spaces are normal (prop. ), Urysohn's lemma (prop. ) says that there exist continuous functions of the form
with the property that
This means in particular that and hence that the support of the function is contained in
By this construction, the set of function already satisfies conditions 1) and 2) on a partition of unity subordinate to from def. . It just remains to normalize these functions so that they indeed sum to unity. To that end, consider the continuous function
defined on by
Notice that the sum on the right has only a finite number of non-zero summands, due to the local finiteness of the cover, so that this is well-defined. Moreover this is again a continuous function, since polynomials are continuous (example ).
Moreover, notice that
because is a cover so that there is with , and since , by the above, and since all contributions to the sum are non-negative.
Hence it makes sense to define the ratios
Since this still satisfies conditions 1) and 2) on a partition of unity (def. ), but by construction this now also satisfies
and hence the remaining condition 3). Therefore
is a partition of unity as required.
We will see various applications of prop. in the discussion of topological vector bundles and of topological manifolds, to which we now turn.
Vector bundles
A (topological) vector bundle is a collection of vector spaces that vary continuously over a topological space. Hence topological vector bundles combine linear algebra with topology. The usual operations of linear algebra, such as direct sum and tensor product of vector spaces, generalize to “parameterized” such operations and on vector bundles over some base space (def. and def. below).
This way a semi-ring of isomorphism classes of topological vector bundles is associated with every topological space. If one adds in formal additive inverses to this semiring (passing to the group completion of the direct sum of vector bundles) one obtains an actual ring, called the topological K-theory of the topological space. This is a fundamental topological invariant that plays a central role in algebraic topology.
A key class of examples of topological vector bundles are the tangent bundles of differentiable manifolds to which we turn below. For these the vector space associated with every point is the “linear approximation” of the base space at that point.
Topological vector bundles are particularly well behaved over paracompact Hausdorff spaces, where the existence of partitions of unity (by prop. above) allows to perform global operations on vector bundles by first performing them locally and then using the partition of unity to continuously interpolate between these local constructions. This is one reason why the definition of topological manifolds below demands them to be paracompact Hausdorff spaces.
The combination of topology with linear algebra begins in the evident way, in the same vein as the concept of topological groups (def. ); we “internalize” definitions from linear algebra into the cartesian monoidal category Top (remark , remark ):
Definition
(topological ring and topological field)
A topological ring is
-
a ring ,
-
a topology on the underlying set of the ring, making it a topological space (def. )
such that
-
is a topological group with respect to (def. );
-
also the multiplication is a continuous function with respect to and the product topology (example ).
A topological ring is a topological field if
-
is a field;
-
the function assigning multiplicative inverses is a continuous function with respect to the subspace topology.
Remark
There is a redundancy in def. : For a topological ring the continuity of the assignment of additive inverses is already implied by the continuity of the multiplication operation, since
Example
(real and complex numbers are topological fields)
The fields of real numbers and of complex numbers are topological fields (def. ) with respect to their Euclidean metric topology (example , example )
That the operations on these fields are all continuous with respect to the Euclidean topology is the statement that rational functions are continuous on the domain of definition inside Euclidean space (example .)
Definition
Let
-
be a topological field (def. )
-
be a topological space.
Then a topological -vector bundle over is
-
for each the structure of a finite-dimensional -vector space on the pre-image
called the fiber of the bundle over
such that this is locally trivial in that there exists:
-
an open cover ,
-
for each an and a homeomorphism
from the product topological space of with the topological field to the restriction of over , such that
-
is a function over in that , hence in that
-
is a linear map in each fiber in that
-
Here is the diagram of continuous functions that illustrates these conditions:
Often, but not always, it is required that the numbers are all equal to some , for all , hence that the vector space fibers all have the same dimension. In this case one says that the vector bundle has rank . (Over a connected topological space this is automatic, but the fiber dimension may be distinct over distinct connected components.)
For and two topological vector bundles over the same base space, then a homomorphism between them is
such that
-
respects the projections: ;
-
for each we have that is a linear map.
Remark
(category of topological vector bundles)
For a topological space and a topological field, there is the category whose
-
objects are the topological -vector bundles over ,
-
morphisms are the topological -vector bundle homomorphisms
This category is usually denoted or just when the ground field is understood (often: the real numbers, next often the complex numbers).
The set of isomorphism classes in this category (topological vector bundles modulo invertible homomorphism between them) we denote by .
There is a larger category, where we allow the morphisms to involve a continuous function between base spaces, so that the continuous functions on total spaces are, besides being fiberwise linear, required to make the following diagram commute:
Remark
(some terminology)
For one speaks of real vector bundles.
For one speaks of complex vector bundles.
For one speaks of line bundles, in particular of real line bundles and of complex line bundles.
Remark
(any two topological vector bundles have local trivialization over a common open cover)
Let and be two topological vector bundles (def. ). Then there always exists an open cover such that both bundles have a local trivialization over this cover.
Proof
By definition we may find two possibly different open covers and with local tivializations and .
The joint refinement of these two covers is the open cover given by the intersections of the original patches:
The original local trivializations restrict to local trivializations on this finer cover
and
Example
(topological trivial vector bundle and (local) trivialization)
For any topological space, and , we have that the product topological space
canonically becomes a topological vector bundle over (def. ). A local trivialization is given over the trivial cover by the identity function .
This is called the trivial vector bundle of rank over .
Given any topological vector bundle , then a choice of isomorphism to a trivial bundle (if it exists)
is called a trivialization of . A vector bundle for which a trivialization exists is called trivializable.
Accordingly, the local triviality condition in the definition of topological vector bundles (def. ) says that they are locally isomorphic to the trivial vector bundle. One also says that the data consisting of an open cover and the homeomorphisms
as in def. constitute a local trivialization of .
Example
(section of a topological vector bundle)
Let be a topological vector bundle (def. ).
Then a homomorphism of vector bundles from the trivial line bundle (example , remark )
is, by fiberwise linearity, equivalently a continuous function
such that
Such functions are called sections (or cross-sections) of the vector bundle .
Namely by is necessarily of the form
for a unique such section .
Example
(topological vector sub-bundle)
Given a topological vector bundle (def. ), then a sub-bundle is a homomorphism of topological vector bundles over
such that for each point this is a linear embedding of fibers
(This is a monomorphism in the category of topological vector bundles over (remark ).)
The archetypical example of vector bundles are the tautological line bundles on projective spaces:
Definition
(topological projective space)
Let be a topological field (def. ) and . Consider the product topological space , let be the topological subspace which is the complement of the origin, and consider on its underlying set the equivalence relation which identifies two points if they differ by multiplication with some (necessarily non-zero):
The equivalence class is traditionally denoted
Then the projective space is the corresponding quotient topological space
For this is called real projective space ;
for this is called complex projective space .
Examples
The first complex projective space (def. ) is homeomorphic to the Euclidean 2-sphere (example )
Under this identification one also speaks of the Riemann sphere.
Definition
(standard open cover of topological projective space)
For the standard open cover of the projective space (def. ) is
with
To see that this is an open cover:
-
This is a cover because with the origin removed in at every point at least one of the has to be non-vanishing.
-
These subsets are open in the quotient topology , since their pre-image under the quotient co-projection coincides with the pre-image under the projection onto the th coordinate in the product topological space .
Example
(canonical cover of Riemann sphere is the stereographic projection)
Under the identification of the first complex projective space as the Riemann sphere, from example , the canonical cover from def. is the cover by the two stereographic projections from example .
Definition
(topological tautological line bundle)
For a topological field (def. ) and , the tautological line bundle over the projective space is topological -line bundle (remark ) whose total space is the following subspace of the product space (example ) of the projective space (def. ) with :
where is the -linear span of .
(The space is the space of pairs consisting of the “name” of a -line in together with an element of that -line)
This is a bundle over projective space by the projection function
Proposition
(tautological topological line bundle is well defined)
The tautological line bundle in def. is well defined in that it indeed admits a local trivialization.
Proof
We claim that there is a local trivialization over the canonical cover of def. . This is given for by
This is clearly a bijection of underlying sets.
To see that this function and its inverse function are continuous, hence that this is a homeomorphism notice that this map is the extension to the quotient topological space of the analogous map
This is a polynomial function on Euclidean space and since polynomials are continuous, this is continuous. Similarly the inverse function lifts to a rational function on a subspace of Euclidean space, and since rational functions are continuous on their domain of definition, also this lift is continuous.
Therefore by the universal property of the quotient topology, also the original functions are continuous.
Transition functions
We discuss how topological vector bundles are equivalently given by cocycles (def. below) in Cech cohomology (def. ) constituted by their transition functions (def. below). This allows to make precise the intuition that vector bundles are precisely the result of “continuously gluing” trivial vector bundles onto each other“ (prop. below).
This gives a “local-to-global principle” for constructions on vector bundles. For instance it allows to easily obtain concepts of direct sum of vector bundles and tensor product of vector bundles (def. and def. below) by applying the usual operations from linear algebra on a local trivialization and then re-gluing the result via the combined transition functions.
The definition of Cech cocycles is best stated with the following terminology in hand:
Definition
(continuous functions on open subsets with values in the general linear group)
For , regard the general linear group as a topological group with its standard topology, given as the Euclidean subspace topology via or as the subspace topology of the compact-open topology on the mapping space. (That these topologies coincide is the statement of this prop..
For a topological space, we write
for the assignment that sends an open subset to the set of continuous functions (for equipped with its subspace topology), regarded as a group via the pointwise group operation in :
Moreover, for an inclusion of open subsets, and for , we write
for the restriction of the continuous function from to .
Remark
In the language of category theory the assignment from def. of sets continuous functions to open subsets and the restriction operations between these is called a sheaf of groups on the site of open subsets of .
Definition
Given a topological vector bundle as in def. and a choice of local trivialization (example ) there are for induced continuous functions
to the general linear group (as in def. ) given by composing the local trivialization isomorphisms:
These are called the transition functions for the given local trivialization.
These functions satisfy a special property:
Definition
Let be a topological space.
A normalized Cech cocycle of degree 1 with coefficients in (def. ) is
-
an open cover
such that
-
(normalization) (the constant function on the neutral element in ),
-
(cocycle condition) .
Write
for the set of all such cocycles for given and write
for the disjoint union of all these cocycles as varies.
Example
(transition functions are Cech cocycles)
Let be a topological vector bundle (def. ) and let , be a local trivialization (example ).
Then the set of induced transition functions according to def. is a normalized Cech cocycle on with coefficients in , according to def. .
Proof
This is immediate from the definition:
and
Conversely:
Example
(topological vector bundle constructed from a Cech cocycle)
Let be a topological space and let a Cech cocycle on according to def. , with open cover and component functions .
This induces an equivalence relation on the product topological space
(of the disjoint union space of the patches regarded as topological subspaces with the product space ) given by
Write
for the resulting quotient topological space. This comes with the evident projection
which is a continuous function (by the universal property of the quotient topological space construction, since the corresponding continuous function on the un-quotiented disjoint union space respects the equivalence relation). Moreover, each fiber of this map is identified with , and hence canonically carries the structure of a vector space.
Finally, the quotient co-projections constitute a local trivialization of this vector bundle over the given open cover.
Therefore is a topological vector bundle (def. ). We say it is the topological vector bundle glued from the transition functions.
Remark
(bundle glued from Cech cocycle is a coequalizer)
Stated more category theoretically, the constructure of a topological vector bundle from Cech cocycle data in example is a universal construction in topological spaces, namely the coequalizer of the two morphisms
in the category of vector space objects in the slice category . Here the restriction of to the coproduct summands is induced by inclusion:
and the restriction of to the coproduct summands is via the action of the transition functions:
In fact, extracting transition functions from a vector bundle by def. and constructing a vector bundle from Cech cocycle data as above are operations that are inverse to each other, up to isomorphism.
Proposition
(topological vector bundle reconstructed from its transition functions)
Let be a topological vector bundle (def. ), let be an open cover of the base space, and let be a local trivialization.
Write
for the corresponding transition functions (def. ). Then there is an isomorphism of vector bundles over
from the vector bundle glued from the transition functions according to def. to the original bundle , whose components are the original local trivialization isomorphisms.
Proof
By the universal property of the disjoint union space (coproduct in Top), continuous functions out of them are equivalently sets of continuous functions out of every summand space. Hence the set of local trivializations may be collected into a single continuous function
By construction this function respects the equivalence relation on the disjoint union space given by the transition functions, in that for each we have
By the universal property of the quotient space coprojection this means that uniquely extends to a continuous function on the quotient space such that the following diagram commutes
It is clear that this continuous function is a bijection. Hence to show that it is a homeomorphism, it is now sufficient to show that this is an open map (by prop. ).
So let be a subset in the quotient space which is open. By definition of the quotient topology this means equivalently that its restriction to is open for each . Since the are homeomorphisms, it follows that the images are open. By the nature of the subspace topology, this means that these images are open also in . Therefore also the union is open.
Here are some basic examples of vector bundles constructed from transition functions.
Example
Let
be the circle with its Euclidean subspace metric topology. Consider the open cover
with
for any .
Define a Cech cohomology cocycle (remark ) on this cover by
Since there are no non-trivial triple intersections, all cocycle conditions are evidently satisfied.
Accordingly by example these functions define a vector bundle.
The total space of this bundle is homeomorphic to (the interior, def. of) the Moebius strip from example .
Example
(basic complex line bundle on the 2-sphere)
Let
be the 2-sphere with its Euclidean subspace metric topology. Let
be the two complements of antipodal points
Define continuous functions
Since there are no non-trivial triple intersections, the only cocycle condition is
which is clearly satisfied.
The complex line bundle this defined is called the basic complex line bundle on the 2-sphere.
With the 2-sphere identified with the complex projective space (the Riemann sphere), the basic complex line bundle is the tautological line bundle (example ) on .
Example
Generally, for , then the n-sphere may be covered by two open hemispheres intersecting in an equator of the form . A vector bundle is then defined by specifying a single function
This is called the clutching construction of vector bundles over n-spheres.
Using transition functions, it is immediate how to generalize the operations of direct sum and of tensor product of vector spaces to vector bundles:
Definition
(direct sum of vector bundles)
Let be a topological space, and let and be two topological vector bundles over .
Let be an open cover with respect to which both vector bundles locally trivialize (this always exists: pick a local trivialization of either bundle and form the joint refinement of the respective open covers by intersection of their patches). Let
be the transition functions of these two bundles with respect to this cover.
For write
be the pointwise direct sum of these transition functions
Then the direct sum bundle is the one glued from this direct sum of the transition functions (by this construction):
Definition
(tensor product of vector bundles)
Let be a topological space, and let and be two topological vector bundles over .
Let be an open cover with respect to which both vector bundles locally trivialize (this always exists: pick a local trivialization of either bundle and form the joint refinement of the respective open covers by intersection of their patches). Let
be the transition functions of these two bundles with respect to this cover.
For write
be the pointwise tensor product of vector spaces of these transition functions
Then the tensor product bundle is the one glued from this tensor product of the transition functions (by this construction):
And so forth. For instance:
Definition
(inner product on vector bundles)
Let
-
be a topological field (such as the real numbers or complex numbers with their Euclidean metric topology ),
-
be a topological space,
-
a topological vector bundle over (over , say).
Then an inner product on is
-
a vector bundle homomorphism
from the tensor product of vector bundles of with itself to the trivial line bundle
such that
-
for each point the function
is an inner product on the fiber vector space, hence a positive-definite symmetric bilinear form.
Next we need to see how the transition functions behave under isomorphisms of vector bundles.
Definition
(coboundary between Cech cocycles )
Let be a topological space and let be two Cech cocycles (def. ), given by
-
and two open covers,
-
and the corresponding component functions.
Then a coboundary between these two cocycles is
-
the condition that ,
-
an open cover ,
-
functions and such that
such that
-
,
hence such that the following diagrams of linear maps commute for all and :
Say that two Cech cocycles are cohomologous if there exists a coboundary between them.
Example
(refinement of a Cech cocycle is a coboundary)
Let be a topological space and let be a Cech cocycle as in def. , with respect to some open cover , given by component functions .
Then for a refinement of the given open cover, hence an open cover such that there exists a function with , then
are the components of a Cech cocycle which is cohomologous to .
Proposition
(isomorphism of topological vector bundles induces Cech coboundary between their transition functions)
Let be a topological space, and let be two Cech cocycles as in def. .
Every isomorphism of topological vector bundles
between the vector bundles glued from these cocycles according to def. induces a coboundary between the two cocycles,
Proof
By example we may assume without restriction that the two Cech cocycles are defined with respect to the same open cover (for if they are not, then by example both are cohomologous to cocycles on a joint refinement of the original covers and we may argue with these).
Accordingly, by example the two bundles and both have local trivializations of the form
and
over this cover. Consider then for the function
hence the unique function making the following diagram commute:
This induces for all the following composite commuting diagram
By construction, the two horizonal composites of this diagram are pointwise given by the components and of the cocycles and , respectively. Hence the commutativity of this diagram is equivalently the commutativity of these diagrams:
for all and . By def. this exhibits the required coboundary.
Definition
Let be a topological space. The relation on Cech cocycles of being cohomologous (def. ) is an equivalence relation on the set of Cech cocycles (def. ).
Write
for the resulting set of equivalence classes. This is called the Cech cohomology of in degree 1 with coefficients in .
Proposition
(Cech cohomology computes isomorphism classes of topological vector bundle)
Let be a topological space.
The construction of gluing a topological vector bundle from a Cech cocycle (example ) constitutes a bijection between the degree-1 Cech cohomology of with coefficients in (def. ) and the set of isomorphism classes of topological vector bundles on (def. , remark ):
Proof
First we need to see that the function is well defined, hence that if cocycles are related by a coboundary, (def. ), then the vector bundles and are related by an isomorphism.
Let be the open cover with respect to which the coboundary is defined, with refining functions and . Let and be the corresponding restrictions of the canonical local trivilizations of the two glued bundles.
For define
Observe that for and the coboundary condition implies that
because in the diagram
the vertical morphism in the middle on the right is unique, by the fact that all other morphisms in the diagram on the right are invertible.
Therefore by example there is a unique vector bundle homomorphism
given for all by . Similarly there is a unique vector bundle homomorphism
given for all by . Hence this is the required vector bundle isomorphism.
Finally to see that the function from Cech cohomology classes to isomorphism classes of vector bundles thus defined is a bijection:
By prop. the function is surjective, and by prop. it is injective.
Properties
We discuss some basic general properties of topological vector bundles.
Lemma
(homomorphism of vector bundles is isomorphism as soon as it is a fiberwise isomorphism)
Let and be two topological vector bundles (def. ).
If a homomorphism of vector bundles restricts on the fiber over each point to a linear isomorphism
then is already an isomorphism of vector bundles.
Proof
It is clear that has an inverse function
of underlying sets which is a function over : Over each it it the linear inverse .
What we need to show is that this is a continuous function.
By remark we find an open cover over which both bundles have a local trivialization.
Restricted to any patch of this cover, the homomorphism induces a homomorphism of trivial vector bundles
Also the are fiberwise invertible, hence are continuous bijections. We claim that these are homeomorphisms, hence that their inverse functions are also continuous.
To this end we re-write the a little. First observe that by the universal property of the product topological space and since they fix the base space , the are equivalently given by a continuous function
as
Moreover since is locally compact (as every metric space), the mapping space adjunction says (by prop. ) that there is a continuous function
(with the set of continuous functions equipped with the compact-open topology) which factors via the evaluation map as
By assumption of fiberwise linearity the functions in fact take values in the general linear group
and this inclusion is a homeomorphism onto its image (by this prop.).
Since passing to inverse matrices
is a rational function on its domain inside Euclidean space and since rational functions are continuous on their domain of definition, it follows that the inverse of
is a continuous function.
To conclude that also is a continuous function we make use prop. to find an isomorphism between and a quotient topological space of the form
Hence is equivalently a function on this quotient space, and we need to show that as such it is continuous.
By the universal property of the disjoint union space (the coproduct in Top) the set of continuous functions
corresponds to a single continuous function
These functions respect the equivalence relation, since for each we have
Therefore by the universal property of the quotient topological space , these functions extend to a unique continuous function such that the following diagram commutes:
This unique function is clearly (by pointwise inspection) and therefore is continuous.
Example
(fiberwise linearly independent sections trivialize a vector bundle)
If a topological vector bundle of rank admits sections (example )
that are linearly independent at each point , then is trivializable (example ). In fact, with the sections regarded as vector bundle homomorphisms out of the trivial vector bundle of rank (according to example ), these sections are the trivialization
This is because their linear independence at each point means precisely that this morphism of vector bundles is a fiber-wise linear isomorphism and therefore an isomorphism of vector bundles by lemma .
(…)
Manifolds
A topological manifold is a topological space which is locally homeomorphic to a Euclidean space (def. below), but which may globally look very different. These are the kinds of topological spaces that are really meant when people advertise topology as “rubber-sheet geometry”.
If the gluing functions which relate the Euclidean local charts of topological manifolds to each other are differentiable functions, for a fixed degree of differentiability, then one speaks of differentiable manifolds (def below) or of smooth manifolds if the gluing functions are arbitrarily differentiable.
Accordingly, a differentiable manifold is a space to which the tools of infinitesimal analysis may be applied locally. In particular we may ask whether a continuous function between differentiable manifolds is differentiable by computing its derivatives pointwise in any of the Euclidean coordinate charts. This way differential and smooth manifolds are the basis for what is called differential geometry. (They are the analogs in differential geometry of what schemes are in algebraic geometry.)
Basic examples of smooth manifolds are the n-spheres (example below), the projective spaces (example below). and the general linear group (example ) below.
The definition of topological manifolds (def. below) involves two clauses: The conceptual condition is that a manifold is locally Euclidean topological space (def. below). On top of this one demands as a technical regularity condition paracompact Hausdorffness, which serves to ensure that manifolds behave well. Therefore we first consider locally Euclidean spaces in themselves.
Definition
(locally Euclidean topological space)
A topological space is locally Euclidean if every point has an open neighbourhood which, as a subspace (example ), is homeomorphic (def. ) to the Euclidean space (example ) with its metric topology (def. ):
The “local” topological properties of Euclidean space are inherited by locally Euclidean spaces:
Proposition
(locally Euclidean spaces are -separated, sober, locally compact, locally connected and locally path-connected topological spaces)
Let be a locally Euclidean space (def. ). Then
-
satisfies the separation axiom (def. );
-
is sober (def. );
-
is locally compact in the weak sense of def. .
-
is locally connected (def. ),
-
is locally path-connected (def. ).
Proof
Regarding the first statement:
Let be two distinct points in the locally Euclidean space. We need to show that there is an open neighbourhood around that does not contain .
By definition, there is a Euclidean open neighbourhood around . If does not contain , then it already is an open neighbourhood as required. If does contain , then are equivalently two distinct points in . But Euclidean space, as every metric space, is (example , prop. ), and hence we may find an open neighbourhood not containing . By the nature of the subspace topology, is an open neighbourhood as required.
Regarding the second statement:
We need to show that the map
that sends points to the topological closure of their singleton sets is a bijection with the set of irreducible closed subsets. By the first statement above the map is injective (via lemma ). Hence it remains to see that every irreducible closed subset is the topological closure of a singleton. We will show something stronger: every irreducible closed subset is a singleton.
Let be an open proper subset such that if there are two open subsets with then or . By prop ) we need to show that there exists a point such that it its complement.
Now since is a proper subset, and since the locally Euclidean space is covered by Euclidean neighbourhoods, there exists a Euclidean neighbourhood such that is a proper subset. In fact this still satisfies the condition that for then implies or . Accordingly, by prop. , it follows that is an irreducible closed subset of Euclidean space. Sine metric spaces are sober topological space as well as -separated (example , prop. ), this means that there exists such that .
In conclusion this means that the restriction of an irreducible closed subset in to any Euclidean chart is either empty or a singleton set. This means that the irreducible closed subset must be a disjoint union of singletons that are separated by Euclidean neighbourhoods. But by irreducibiliy, this union has to consist of just one point.
Regarding the third statement:
Let be a point and let be an open neighbourhood. We need to find a compact neighbourhood .
By assumption there exists a Euclidean open neighbourhood . By definition of the subspace topology the intersection is still open as a subspace of and hence is an open neighbourhood of .
Since Euclidean spaces are locally compact (example ), there exists a compact neighbourhood (for instance a sufficiently small closed ball around , which is compact by the Heine-Borel theorem, prop. ). Now since continuous images of compact spaces are compact prop. , it follows that also is a compact neighbourhood.
Regarding the last two statements:
We need to show that for every point and every [neighbourhood there exists a neighbourhood which is and a neighbourhood which is .]
By local Euclideanness there exists a chart . Since Euclidean space is locally connected and locally path-connected (def. ), there is a connected and a path-connected neighbourhood of the pre-image contained in the pre-image . Since continuous images of connected spaces are connected (prop. ), and since continuous images of path-connected spaces are path-connected (prop. ), the images of these neighbourhoods under are neighbourhoods of as required.
It follows immediately from prop. via prop. that:
Proposition
(connected locally Euclidean spaces are path-connected)
For a locally Euclidean space (def. ) the connected components (def. ) coincide with the path-connected components (def. ).
But the “global” topological properties of Euclidean space are not generally inherited by locally Euclidean spaces. This sounds obvious, but notice that also Hausdorff-ness is a “global property”:
Remark
(locally Euclidean spaces are not necessarily )
It might superficially seem that every locally Euclidean space (def. ) is necessarily a Hausdorff topological space, since Euclidean space, like any metric space, is Hausdorff, and since by definition the neighbourhood of every point in a locally Euclidean spaces looks like Euclidean space.
But this is not so, see the counter-example below, Hausdorffness is a “non-local condition”, as opposed to the and separation axioms.
Nonexample
(non-Hausdorff locally Euclidean spaces)
An example of a locally Euclidean space (def. ) which is a non-Hausdorff topological space, is the line with two origins (example ).
Therefore we will explicitly impose Hausdorffness on top of local Euclidean-ness. This implies the equivalence of following further regularity properties:
Proposition
(equivalence of regularity conditions for locally Euclidean Hausdorff spaces)
Let be a locally Euclidean space (def. ) which is Hausdorff (def. ).
Then the following are equivalent:
-
is sigma-compact (def. ).
-
is second-countable (def. ).
-
is paracompact (def. ) and has a countable set of connected components (def. ).
Proof
First, observe that is locally compact in the strong sense of def. : By prop. every locally Euclidean space is locally compact in the weak sense that every neighbourhood contains a compact neighbourhood, but since is assumed to be Hausdorff, this implies the stronger statement by prop. .
1) 2)
Let be sigma-compact. We show that then is second-countable:
By sigma-compactness there exists a countable set of compact subspaces. By being locally Euclidean, each admits an open cover by restrictions of Euclidean spaces. By their compactness, each has a subcover
with a finite set. Since countable unions of countable sets are countable, we have obtained a countable cover of by Euclidean spaces . Now Euclidean space itself is second countable (by example ), hence admits a countable set of base open sets. As a result the union is a base of opens for . But this is a countable union of countable sets, and since countable unions of countable sets are countable we have obtained a countable base for the topology of . This means that is second-countable.
1) 3)
Let be sigma-compact. We show that then is paracompact with a countable set of connected components:
Since locally compact and sigma-compact spaces are paracompact (prop. ), it follows that is paracompact. By local connectivity (prop. ) is the disjoint union space of its connected components (def. , lemma ). Since, by the previous statement, is also second-countable it cannot have an uncountable set of connected components. (Because there must be at least one base open contained in every connected component.)
2) 1) Let be second-countable, we need to show that it is sigma-compact.
This follows since locally compact and second-countable spaces are sigma-compact (lemma ).
3) 1)
Now let be paracompact with countably many connected components. We show that is sigma-compact.
By local compactness, there exists an open cover such that the topological closures constitute a cover by compact subspaces. By paracompactness there is a locally finite refinement of this cover. Since paracompact Hausdorff spaces are normal (prop. ), the shrinking lemma applies (lemma ) to this refinement and yields a locally finite open cover
as well as a locally finite cover by closed subsets. Since this is a refinement of the original cover, all the are contained in one of the compact subspaces . Since subsets are closed in a closed subspace precisely if they are closed in the ambient space (lemma ), the are also closed as subsets of the . Since closed subsets of compact spaces are compact (lemma ) it follows that the are themselves compact and hence form a locally finite cover by compact subspaces.
Now fix any .
We claim that for every there is a finite sequence of indices with the property that for all .
To see this, first observe that it is sufficient to show sigma-compactness for the case that is connected. From this the general statement follows since countable unions of countable sets are countable. Hence assume that is connected. It follows from prop. that is path-connected.
Hence for any and there is a path (def. ) connecting with . Since the closed interval is compact (example ) and since continuous images of compact spaces are compact (prop. ), it follows that there is a finite subset of the that covers the image of this path. This proves the claim.
It follows that there is a function
which sends each to the minimum natural number as above.
We claim now that for all the preimage of under this function is a finite set. Since countable unions of countable sets are countable this means that serves as a countable enumeration of the set and hence implies that is a countable cover of by compact subspaces, hence that is sigma-compact.
We prove this last claim by induction. It is true for by construction, since . Assume it is true for some , hence that is a finite set. Since finite unions of compact subspaces are again compact (example ) it follows that
is compact. By local finiteness of the , every point has an open neighbourhood that intersects only a finite set of the . By compactness of , the cover has a finite subcover. In conclusion this implies that only a finite number of the intersect .
Now by definition is a subset of those which intersect , and hence itself finite.
This finally gives a good idea of what the definition of topological manifolds should be:
Definition
A topological manifold is a topological space which is
-
locally Euclidean (def. ),
-
paracompact Hausdorff (def. , def. ).
If the Euclidean neighbourhoods of the points are all of dimension for some , then the topological manifold is said to be of dimension , too. Sometimes one also speaks of an “-fold” in this case.
Remark
(varying terminology regarding “topological manifold”)
Often a topological manifold (def. ) is required to be second-countable (def. ) or sigma-compact (def. ). But by prop. both conditions are implied by def. as soon as there is a countable set of connected components. Manifolds with uncountably many connected components are rarely considered in practice. The restriction to countably many connected components is strictly necessary for several important theorems (beyond the scope of our discussion here) such as:
Besides the trivial case of Euclidean spaces themselves, we discuss here three main classes of examples of manifolds:
-
n-spheres (example below)
-
projective spaces (example below)
-
general linear groups (example ) below.
Since all these examples are not just topological manifolds but naturally carry also the structure of differentiable manifolds, we first consider this richer definition before turning to the examples:
Definition
(local chart, atlas and gluing function)
Given an -dimensional topological manifold (def. ), then
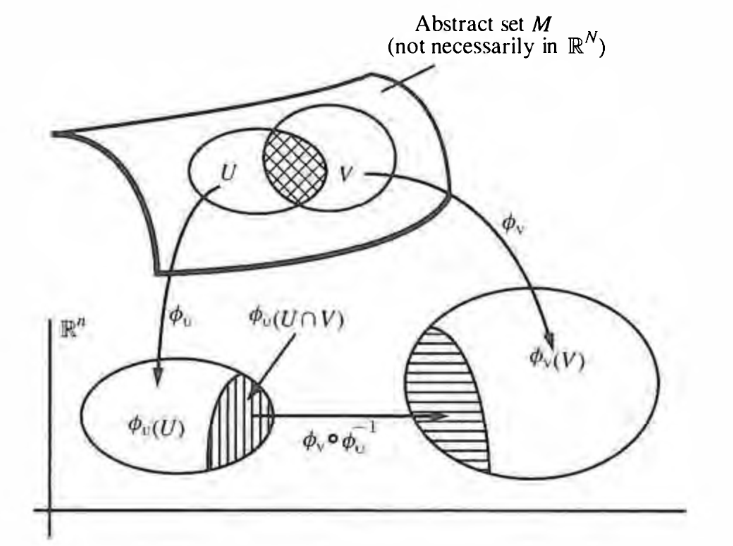
-
An open subset and a homeomorphism from the -dimensional Euclidean space is also called a local coordinate chart of .
-
An open cover of by local charts is called an atlas of the topological manifold.
-
Given such an atlas then for each the induced homeomorphism
is called the coordinate transformation or gluing function from chart to chart .
graphics grabbed from Frankel
Next we consider the case that the gluing functions of a topological manifold are differentiable functions in which case one speaks of a differentiable manifold (def. below). For convenience we first recall the definition of differentiable functions between Euclidean spaces:
Definition
(differentiable functions between Euclidean spaces)
Let and let be an open subset of Euclidean space (example ).
Then a function is called differentiable at if there exists a linear map such that the following limit exists and vanishes as approaches zero “from all directions at once”:
This means that for all there exists an open neighbourhood of such that whenever we have .
We say that is differentiable on a subset of if is differentiable at every , and we say that is differentiable if is differentiable on all of . We say that is continuously differentiable if it is differentiable and is a continuous function.
The function is called the derivative or differential of at .
More generally, let and let be an open subset.
Then a function is differentiable if for all the component function
is differentiable in the previous sense
In this case, the derivatives of the assemble into a linear map of the form
If the derivative exists at each , then it defines itself a function
to the space of linear maps from to , which is canonically itself a Euclidean space. We say that is twice continuously differentiable if is continuously differentiable.
Generally then, for the function is called -fold continuously differentiable or of class if for all the -fold differential exists and is a continuous function.
Finally, if is -fold continuously differentiable for all then it is called a smooth function or of class .
Of the various properties satisfied by differentiation, the following plays a special role in the theory of differentiable manifolds (notably in the discussion of their tangent bundles, def. below):
Proposition
(chain rule for differentiable functions between Euclidean spaces)
Let and let
be two differentiable functions (def. ). Then the derivative of their composite is the composite of their derivatives:
Definition
(differentiable manifold and smooth manifold)
For then a -fold differentiable manifold or -manifold for short is
-
a topological manifold (def. );
-
an atlas (def. ) all whose gluing functions are times continuously differentiable.
A -fold differentiable function between -fold differentiable manifolds
is
such that
-
for all and then
is a -fold differentiable function between open subsets of Euclidean space.
(Notice that this in in general a non-trivial condition even if and is the identity function. In this case the above exhibits a passage to a different, but equivalent, differentiable atlas.)
If a manifold is differentiable for all , then it is called a smooth manifold. Accordingly a continuous function between differentiable manifolds which is -fold differentiable for all is called a smooth function,
Remark
(category Diff of differentiable manifolds)
In analogy to remark there is a category called Diff (or similar) whose objects are -differentiable manifolds and whose morphisms are -differentiable functions, for given .
The analog of the concept of homeomorphism (def. ) is now this:
Definition
Given smooth manifolds and (def. ), then a smooth function
is called a diffeomorphism, if there is an inverse function
which is also a smooth function (hence if is an isomorphism in the category Diff from remark ).
Remark
(basic properties of diffeomorphisms)
Let be differentiable manifolds (def. ). Let
be a diffeomorphisms (def. ) with inverse differentiable function
Then:
-
is in particular a homeomorphism (def. ) between the underlying topological spaces.
Because, by definition, is in particular a continuous function, as is its inverse function .
-
The derivative (def. ) of takes values in invertible linear maps, i.e. is a linear isomorphism for all .
This is because by the chain rule (prop. ) the defining equations
imply that
Beware that just as with homeomorphisms (counter-example ) a differentiable bijective function of underlying sets need not be a diffeomorphism, see example below.
It is important to note that while being a topological manifold is just a property of a topological space, a differentiable manifold carries extra structure encoded in the atlas:
Definition
Let be a topological manifold (def. ) and let
be two atlases (def. ), both making into a smooth manifold (def. ).
Then there is a diffeomorphism (def. ) of the form
precisely if the identity function on the underlying set of constitutes such a diffeomorphism. (Because if is a diffeomorphism, then also is a diffeomorphism.)
That the identity function is a diffeomorphism between equipped with these two atlases means, by definition , that
Notice that the functions on the right may equivalently be written as
showing their analogy to the gluing functions within a single atlas (def. ).
Hence diffeomorphism induces an equivalence relation on the set of smooth atlases that exist on a given topological manifold . An equivalence class with respect to this equivalence relation is called a smooth structure on .
Now we finally discuss examples of manifolds.
Example
(Cartesian space as a smooth manifold)
For then the Cartesian space equipped with the atlas consisting of the single chart
is a smooth manifold, in particularly a -fold differentiable manifold for every according to def. .
Similarly the open disk becomes a smooth manifold when equipped with the atlas whose single chart is the homeomorphism . from example .
Counter-Example
(bijective smooth function which is not a diffeomorphism)
Regard the real line as a smooth manifold via example . Consider the function
This is clearly a smooth function and its underlying function of sets is a bijection.
But it is not a diffeomorphism (def. ): The derivative vanishes at , and hence it cannot be a diffeomorphism by remark .
Example
(n-sphere as a smooth manifold)
For all , the n-sphere becomes a smooth manifold, with atlas consisting of the two local charts that are given by the inverse functions of the stereographic projection from the two poles of the sphere onto the equatorial hyperplane
By the formula given in the proof of prop. the induced gluing function are rational functions and hence smooth functions.
Finally the -sphere is a paracompact Hausdorff topological space. Ways to see this include:
-
is a compact subspace by the Heine-Borel theorem (prop. ). Compact spaces are also paracompact (example ). Moreover, Euclidean space, like any metric space, is Hausdorff (example ), and subspaces of Hausdorff spaces are Hausdorff;
-
The -sphere has the structure of a CW-complex (example ) and CW-complexes are paracompact Hausdorff spaces (example ).
Remark
The constructions in example and define smooth structures (def. ) on the topological spaces underlying the Euclidean spaces and the n-spheres . These are clearly the standard smooth structures that are used by default whenever these spaces are used in differential geometry, since the beginning of the topic in the work by Gauss 1827.
But since being a smooth manifold is extra structure on a topological space (as opposed to being a topological manifold, which is just extra property) it makes sense to ask whether and admit other smooth structures besides these standard ones. Remarkably, they do, for special values of the dimension . These are called exotic smooth structures. Here are some results:
In dimension there are no exotic smooth structures: Two smooth manifolds of dimension are diffeomorphic (def. ) as soon as their underlying topological space are homeomorphic (def. ).
For with there is a unique smooth structure on the Euclidean space (the standard one from example ).
There are uncountably many exotic smooth structures on Euclidean 4-space .
For each , there is a finite set of smooth structures on the n-sphere .
It is still unknown whether there is an exotic smooth structure on the 4-sphere .
The only n-spheres with no exotic smooth structure in the range are , , , and .
For more on all of this see at exotic smooth structure.
Example
(open subsets of differentiable manifolds are again differentiable manifolds)
Let be a -fold differentiable manifold (def. ) and let be an open subset of the underlying topological space .
Then carries the structure of a -fold differentiable manifold such that the inclusion map is an open embedding of differentiable manifolds.
Proof
Since the underlying topological space of is locally connected (prop. ) it is the disjoint union space of its connected components (def. , lemma ).
Therefore we are reduced to showing the statement for the case that has a single connected component. By prop. this implies that is second-countable topological space.
Now a subspace of a second-countable Hausdorff space is clearly itself second countable and Hausdorff.
Similarly it is immediate that is still locally Euclidean: since is locally Euclidean every point has a Euclidean neighbourhood in and since is open there exists an open ball in that (itself homeomorphic to Euclidean space) which is a Euclidean neighbourhood of contained in .
For the differentiable structure we pick these Euclidean neighbourhoods from the given atlas. Then the gluing functions for the Euclidean charts on are -fold differentiable follows since these are restrictions of the gluing functions for the atlas of .
Example
(coordinate transformations are diffeomorphisms)
Let be a differentiable manifold (def. ). By example for all the open subsets
canonically are differentiable manifolds themselves. By definition of differentiable manifolds, the coordinate transformation functions
and
both are differentiable functions. Moreover they are bijective functions by assumption and by construction. This means that they are diffeomorphisms (def. ).
Example
(general linear group as a smooth manifold)
For , the general linear group (example ) is a smooth manifold (as an open subspace of Euclidean space , via example and example ).
The group operations, being polynomial functions, are clearly smooth functions with respect to this smooth manifold structure, and thus is a Lie group.
Next we want to show that real projective space and complex projective space (def. ) carry the structure of differentiable manifolds. To that end first re-consider their standard open cover (def. ).
Lemma
(standard open cover of projective space is atlas)
The charts of the standard open cover of projective space, from def. are homeomorphic to Euclidean space .
Proof
If then
and the representatives of the form on the right are unique.
This means that
is a bijection of sets.
To see that this is a continuous function, notice that it is the composite
of the function
with the quotient projection. Now is a polynomial function and since polynomials are continuous, and since the projection to a quotient topological space is continuous, and since composites of continuous functions are continuous, it follows that is continuous.
It remains to see that also the inverse function is continuous. Since
is a rational function, and since rational functions are continuous, it follows, by nature of the quotient topology, that takes open subsets to open subsets, hence that is continuous.
Example
(real/complex projective space is smooth manifold)
For the topological projective space (def. ) is a topological manifold (def. ).
Equipped with the standard open cover of def. regarded as an atlas by lemma , it is a differentiable manifold, in fact a smooth manifold (def. ).
Proof
By lemma is a locally Euclidean space. Moreover, admits the structure of a CW-complex (this prop. and this prop.) and therefore it is a paracompact Hausdorff space since CW-complexes are paracompact Hausdorff spaces. This means that it is a topological manifold.
It remains to see that the gluing functions of this atlas are differentiable functions and in fact smooth functions. But by lemma they are even rational functions.
A differentiable vector bundle is defined just as a topological vector bundle (def. ) only that in addition all structure is required to be differentiable:
Definition
(differentiable vector bundle)
Let be a “differentiable field”, specifically so that is equipped with the canonical differentiable structure from example .
Given a differentiable manifold (def. ), then a differentiable k-vector bundle over of rank is
-
a differentiable function (def. )
-
the structure of a -vector space on the fiber for all
such that there exists
-
an open cover of by open subsets diffeomorphic to Euclidean space with its canonical smooth structure from example (hence an atlas exhibiting the smooth structure of )
-
for each a differentiable function as on the top of this diagram
which makes this diagram commute and which is fiber-wise a linear map.
A homomorphism between differentiable vector bundles and over the same base differentiable manifolds is a differentiable function as in the top of the following diagram
which makes this diagram commute and which restricts to a linear map
on the fiber over each point .
More generally, if and are differentiable vector bundles over possibly different differentiable base manifolds, then a homomorphism is a differentiable function together with a differentiable function that make the diagram
commute and such that
is a linear map for all .
This yields a category (remark ) whose
We write for this category.
Underlying a differentiable vector bundle, is a topological vector bundle (def. ). This yields a forgetful functor
Tangent bundles
Since differentiable manifolds are locally Euclidean spaces whose gluing functions respect the infinitesimal analysis on Euclidean space, they constitute a globalization of infinitesimal analysis from Euclidean space to more general topological spaces. In particular a differentiable manifold has associated to each point a tangent space of vectors that linearly approximate the manifold in the infinitesimal neighbourhood of that point. The union of all these tangent spaces is called the tangent bundle of the differentiable manifold, an example of a topological vector bundle.
The sections of a tangent bundle are therefore a choice of tangent vector for each point of a manifold, varying continuously or in fact differentiably. Such a “field” of tangent vectors is called a tangent vector field.
One may think of this as specifying a direction along the manifold at each point, and accordingly tangent vector fields integrate to groups of diffeomorphisms that “flow along them”. Such flows of tangent vector fields are the basic tool in differential topology.
Finally the tangent bundle, via the frame bundle that is associated to it, is the basis for all actual geometry: By equipping tangent bundles with (torsion-free) “G-structures” one encodes all sorts of flavors of geometry, such as Riemannian geometry, conformal geometry, complex geometry, symplectic geometry, and generally Cartan geometry. This is the topic of differential geometry proper.
Definition
(tangency relation on differentiable curves)
Let be a differentiable manifold of dimension (def. ) and let be a point. On the set of smooth functions of the form
such that
define the relations
and
saying that two such functions are related precisely if either there exists a chart (def. ) around such that (or else for all charts around it is true that) the first derivative of the two functions regarded via the given chart as functions , coincide at (with denoting the canonical coordinate function on ).
Lemma
(tangency is equivalence relation)
The two relations in def. are equivalence relations and they coincide.
Proof
First to see that they coincide, we need to show that if the derivatives in question coincide in one chart , that then they coincide also in any other chart .
For brevity, write
for the intersection of the two charts.
First of all, since the derivative may be computed in any open neighbourhood around , and since the differentiable functions are in particular continuous functions, we may restrict to the open neighbourhood
of and consider the derivatives of the functions
and
But then by definition of the differentiable atlas, there is the differentiable gluing function
such that
for . The chain rule (prop. ) now relates the derivatives of these functions as
Since is a diffeomorphism and since derivatives of diffeomorphisms are linear isomorphisms (by remark ), this says that the derivative of is related to that of by a linear isomorphism , and hence
Finally, that either relation is an equivalence relation is immediate.
Definition
Let be a differentiable manifold and a point. Then a tangent vector on at is an equivalence class of the the tangency equivalence relation (def. , lemma ).
The set of all tangent vectors at is denoted .
Lemma
(real vector space structure on tangent vectors)
For a differentiable manifold of dimension and any point, let be a chart (def. ) of the given atlas, with .
Then there is induced a bijection of sets
from the -dimensional Cartesian space to the set of tangent vectors at (def. ) given by sending to the equivalence class of the following differentiable curve:
For another chart of the atlas with , then the linear isomorphism relating these two identifications is the derivative
of the gluing function of the two charts at the point :
This is also called the transition function between the two local identifications of the tangent space.
If is an atlas of the differentiable manifold , then the set of transition functions
defined this way satisfies the normalized Cech cocycle conditions (def. ) in that for all ,
-
;
-
.
Proof
The bijectivity of the map is immediate from the fact that the first derivative of at is
The formula for the transition function now follows with the chain rule (prop. ):
Similarly the Cech cocycle condition follows by the chain rule:
and the normalization simply by the fact that the derivative of the identity function at any point is the identity linear isomorphism:
Definition
For a differentiable manifold and a point, then the tangent space of at is the set of tangent vectors at (def. ) regarded as a real vector space via lemma .
Example
(tangent bundle of Euclidean space)
If is itself a Euclidean space, then for any two points the tangent spaces and (def. ) are canonically identified with each other:
Using the vector space (or just affine space) structure of we may send every smooth function to the smooth function
This gives a linear bijection
and these linear bijections are compatible, in that for any three points, then
Moreover, by lemma , each tangent space is identified with itself, and this identification in turn is compatible with all the above identifications:
Therefore it makes sense to canonically identify all the tangent spaces of Euclidean space with that Euclidean space itself.
In words, what this identification does is to use the additive group structure on to translate any tangent vector at any point to the corresponding tangent vector at . (Side remark: Hence this construction is not specific to but applies to every Lie group and it fact to every coset space of a Lie group.)
As a result, the collection of all the tangent spaces of Euclidean space is naturally identified with the Cartesian product
equipped with the projection on the first factor
because then the pre-image of a singleton under this projection are canonically identified with the above tangent spaces:
This way, if we equip with the product space topology, then becomes a trivial topological vector bundle (def. ).
This is called the tangent bundle of the Euclidean space regarded as a differentiable manifold.
Remark
(chain rule is functoriality of tangent space construction on Euclidean spaces)
Consider the assignment that sends
-
every Euclidean space to its tangent bundle according to def. ;
-
every differentiable function (def. ) to the function on tangent vectors (def. ) induced by postcomposition with
By the chain rule (prop. ) we have that the derivative of the composite curve is
and hence that under the identification of example this assignment takes to its derivative
Conversely, in the first form above the assignment manifestly respects composition (and identity functions). Viewed from the second perspective this respect for composition is once again the chain rule (prop. ) :
In the language of category theory this says that the assignment
is an endofunctor on the category CartSp whose
-
objects are the Euclidean spaces for ;
-
morphisms are the differentiable functions between these (for any chosen differentiability class with ).
In fact more is true: By example has the structure of a differentiable vector bundle (def. ) and the function is evidently a homomorphism of differentiable vector bundles
Therefore the tangent bundle functor on Euclidean spaces refines to one of the form
to the category of differentiable vector bundles (def. ).
We may now globalize the concept of the tangent bundle of Euclidean space to tangent bundles of general differentiable manifolds:
Definition
(tangent bundle of a differentiable manifold)
Let be a differentiable manifold (def. ) with atlas .
Equip the set of all tangent vectors (def. ), i.e. the disjoint union of the sets of tangent vectors
with a topology (def. ) by declaring a subset to be an open subset precisely if for all charts we have that its preimage under
is open in the Euclidean space (example ) with its metric topology (example ).
Equipped with the function
this is called the tangent bundle of .
Equivalently this means that the tangent bundle is the topological vector bundle (def. ) which is glued (via example ) from the transition functions from lemma :
(Notice that, by examples , each is the tangent bundle of the chart .)
The co-projection maps of this quotient topological space construction constitute an atlas
Lemma
(tangent bundle is differentiable vector bundle)
If is a -times differentiable manifold, then the total space of the tangent bundle def. is a -times differentiable manifold in that
-
The gluing functions of the atlas are -times continuously differentiable.
Moreover, the projection is a -times continuously differentiable function.
In summary this makes a differentiable vector bundle (def. ).
Proof
First to see that is Hausdorff:
Let be two distinct points. We need to produce disjoint openneighbourhoods of these points in . Since in particular are distinct, and since is Hausdorff, there exist disjoint open neighbourhoods and . Their pre-images and are disjoint open neighbourhoods of and , respectively.
Now to see that is paracompact.
Let be an open cover. We need to find a locally finite refinement. Notice that is an open map (by example and example ) so that is an open cover of .
Let now be an atlas for and consider the open common refinement
Since this is still an open cover of and since is paracompact, this has a locally finite refinement
Notice that for each the product topological space is paracompact (as a topological subspace of Euclidean space it is itself locally compact and second countable and since locally compact and second-countable spaces are paracompact, lemma ). Therefore the cover
has a locally finite refinement
We claim now that
is a locally finite refinement of the original cover. That this is an open cover refining the original one is clear. We need to see that it is locally finite.
So let . By local finiteness of there is an open neighbourhood which intersects only finitely many of the . Then by local finiteness of , for each such the point regarded in has an open neighbourhood that intersects only finitely many of the . Hence the intersection is a finite intersection of open subsets, hence still open, and by construction it intersects still only a finite number of the .
This shows that is paracompact.
Finally the statement about the differentiability of the gluing functions and of the projections is immediate from the definitions
Proposition
(differentials of differentiable functions between differentiable manifolds)
Let and be differentiable manifolds and let be a differentiable function. Then the operation of postcomposition, which takes differentiable curves in to differentiable curves in ,
descends at each point to the tangency equivalence relation (def. , lemma ) to yield a function on sets of tangent vectors (def. ), called the differential of at
Moreover:
-
(linear dependence on the tangent vector) these differentials are linear functions with respect to the vector space structure on the tangent spaces from lemma , def. ;
-
(differentiable dependence on the base point) globally they yield a homomorphism of real differentiable vector bundles between the tangent bundles (def. , lemma ), called the global differential of
-
(chain rule) The assignment respects composition in that for , , three differentiable manifolds and for
two composable differentiable functions then their differentials satisfy
Proof
All statements are to be tested on charts of an atlas for and for . On these charts the statement reduces to that of example .
Remark
(tangent functor)
In the language of category theory (remark ) the statement of prop. says that forming tangent bundles of differentiable manifolds and differentials of differentiable functions constitutes a functor
from the category Diff of differentiable manifolds to the category of differentiable real vector bundles.
Definition
Let be a differentiable manifold with differentiable tangent bundle (def. ).
A differentiable section of the tangent bundle is called a (differentiable) vector field on . We write for the real vector space of tangent vector fields on .
Remark
(notation for tangent vectors in a chart)
Under the bijection of lemma one often denotes the tangent vector corresponding to the the -th canonical basis vector of by
because under the identification of tangent vectors with derivations on the algebra of differentiable functions on as above then it acts as the operation of taking the th partial derivative. The general tangent vector corresponding to is then denoted by
Notice that this identification depends on the choice of chart, which is left implicit in this notation.
Sometimes, notably in texts on thermodynamics, one augments this notation to indicate the chart being used by listing the remaining coordinate functions as subscripts. For instance if two functions on a 2-dimensional manifold are used as coordinate functions for a local chart (i.e. so that and ), then one writes
for the tangent vectors and , respectively.
Embeddings
An embedding of topological spaces (def. ) in an inclusion of topological spaces such that the ambient topology induces the included one. An embedding of smooth manifolds (def. below) is similarly meant to be an an inclusion of smooth manifolds, such that the ambient smooth structure induces the included one. In order for this to be the case we need that the tangent spaces include into each other. This is the concept of an immersion of differentiable manifolds (def. below).
It turns out that every connected smooth manifold embeds this way into a Euclidean space. This means that every “abstract” smooth manifold may be thought of as a sub-manifold of Euclidean space. We state and prove the weakest form of this statement (just for compact manifolds and without any bound on the dimension of the ambient Euclidean space) below as prop. . The strong form of this statement is famous as the Whitney embedding theorem (remark below).
Definition
(immersion and submersion of differentiable manifolds)
Let be a differentiable function between differentiable manifolds.
If for each the differential (prop. )
is…
-
…an injective function, then is called an immersion of differentiable manifolds
-
…a surjective function, then is called a submersion of differentiable manifolds.
-
…a bijective function, then is called a local diffeomorphism.
Definition
(embedding of smooth manifolds)
An embedding of smooth manifolds is a smooth function between smooth manifolds and (def. ) such that
-
the underlying continuous function is an embedding of topological spaces (def. );
-
is an immersion (def. ).
A closed embedding is an embedding such that the image is a closed subset.
If is an embedding of smooth manifolds, then is also called a submanifold of .
Nonexample
(immersions that are not embeddings)
Consider an immersion of an open interval into the Euclidean plane (or the 2-sphere) as shown on the right. This is not a embedding of smooth manifolds: around the points where the image crosses itself, the function is not even injective, but even at the points where it just touches itself, the pre-images under of open subsets of do not exhaust the open subsets of , hence do not yield the subspace topology.
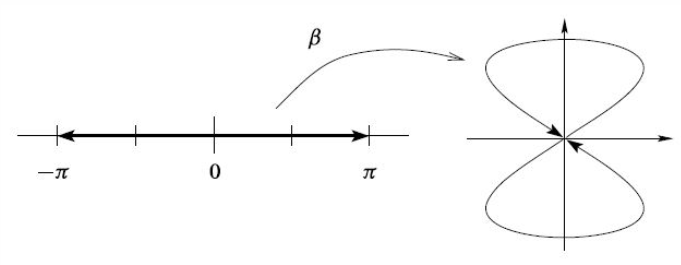
As a concrete examples, consider the function
While this is an immersion and injective, it fails to be an embedding due to the points at “touching” the point at :
Every open neighbourhood in which contains the origin also contains the image for some and hence in the subspace topology on none of the intervals is open, contrary to the actual Euclidean topolgy on .
graphics grabbed from Lee
Proposition
(proper injective immersions are equivalently the closed embeddings)
Let and be smooth manifolds (def. ), and let be a smooth function. Then the following are equivalent
-
is a closed embedding of smooth manifolds (def. ).
Proof
Since topological manifolds are locally compact topological spaces (prop. ), this follows directly since injective proper maps to locally compact spaces are equivalently the closed embeddings by prop. .
We now turn to the construction of embeddings of smooth manifolds into Euclidean spaces (prop. and remark below). To that end we need to consider smooth partitions of unity, which we discuss now (prop. below).
Since manifolds by definition are paracompact Hausdorff spaces, they admit subordinate partitions of unity by continuous functions (by prop. ). But smooth manifolds even admit partitions of unity by smooth bump functions:
Definition
A bump function is a function on Cartesian space , for some with values in the real numbers
such that
-
is smooth (def. );
-
has compact support (def. ).
The main point of interest about bump functions is that they exist, their precise form is usually not of interest. Here is one of many ways to obtain examples:
Example
(a class of bump functions)
For every closed ball (def. ) there exists a bump function (def. ) with support being that closed ball:
Proof
Consider the function
given by
By construction the support of this function is the closed unit ball at the origin, .
We claim that is smooth. That it is smooth away from is clear, hence smoothness only need to be checked at , where it amounts to demanding that all the derivatives of the exponential function vanish as .
But that is the case since
This clearly tends to zero as . A quick way to see this is to consider the inverse function and expand the exponential to see that this tends to as :
The form of the higher derivatives is the same but with higher inverse powers of and so this conclusion remains the same for all derivatives. Hence is smooth.
Now for arbitrary radii define
This is clearly still smooth and .
Finally the function has support the closed ball .
We want to say that a smooth manifold admits subordinate partitions of unity by bump functions (prop. below). To that end we first need to see that it admits refinements of covers by closed balls.
Lemma
(open cover of smooth manifold admits locally finite refinement by closed balls)
Let be a smooth manifold (def. ) and let be an open cover. Then there exists cover
which is a locally finite refinement of with each patch diffeomorphic to a closed ball (def. ) regarded as a subspace of Euclidean space.
Proof
First consider the special case that is compact topological space (def. ).
Let
be a smooth atlas representing the smooth structure on (def. ) (hence an open cover by patches which are diffeomorphic to standard Euclidean space). The intersections
still form an open cover of . Hence for each point there is and with . By the nature of the Euclidean space metric topology, there exists a closed ball around in . Its image is a neighbourhood of diffeomorphic to a closed ball.
The interiors of these balls form an open cover
of which, by construction, is a refinement of . By the assumption that is compact, this has a finite subcover
for a finite set. Hence
is a finite cover by closed balls, hence in particular locally finite, and by construction it is still a refinement of the original cover. This shows the statement for compact.
Now for general , notice that without restriction we may assume that is connected (def. ), for if it is not, then we obtain the required refinement on all of by finding one on each connected component (def. ), and so we are immediately reduced to the connected case.
But, by the proof of prop. , if a locally Euclidean paracompact Hausdorff space is connected, then it is sigma-compact and in fact admits a countable increasing exhaustion
by open subsets whose topological closures
exhaust by compact subspaces .
For , consider the open subspace
which canonically inherits the structure of a smooth manifold by example . As above we find a refinement of the restriction of to this open subset by closed balls and since the further subspace is still compact (example ) there is a finite set such that
is a finite cover of by closed balls refining the original cover.
It follows that the union of all these
is a refinement by closed balls as required. Its local finiteness follows by the fact that each is contained in the “strip” , each strip contains only a finite set of -s and each strip intersects only a finite number of other strips. (Hence an open subset around a point which intersects only a finite number of elements of the refined cover is given by any one of the balls that contain .)
Proposition
(smooth manifolds admit smooth partitions of unity)
Let be a smooth manifold (def. ). Then every open cover has a subordinate partition of unity (def. ) by functions which are smooth functions.
Proof
By lemma the given cover has a locally finite refinement by closed subsets diffeomorphic to closed balls:
Given this, let
be the function which on is given by a smooth bump function (def. , example )
with support :
By the nature of bump functions this is indeed a smooth function on all of . By local finiteness of the cover by closed balls, the function
given by
is well defined (the sum involves only a finite number of non-vanishing contributions), non vanishing (since every point is contained in the support of one of the ) and is smooth (since finite sums of smooth functions are smooth). Therefore if we set
for all then
is a subordinate partition of unity by smooth functions as required.
Now we may finally state and prove the simplest form of the embedding theorem for smooth manifolds:
Proposition
(weak embedding theorem)
For every compact (def. ) smooth manifold of finite dimension (def ), there exists some such that has an embedding of smooth manifolds (def. ) into the Euclidean space of dimension , regarded as a smooth manifold via example :
Proof
Let
be an atlas exhibiting the smooth structure of (def. ), hence an open cover by patches diffeomorphic to Euclidean space. By compactness there exists a finite subset such that
is still an open cover.
Since is a smooth manifold, there exists a partition of unity subordinate to this cover (def. ) with smooth functions (by prop. ).
This we may use to extend the inverse chart identifications
to smooth functions on all of
by setting
The idea now is to use the universal property of the product topological space to combine all these functions to obtain an injective function of the form
This function is an immersion: On the interior of the support of the bump functions the product functions have smooth inverses and therefore their differentials have vanishing kernel.
Hence it remains to see that the function is also an embedding of topological spaces.
Observe that it is an injective function: If two points have the same image, this means that they have the same image under all the . But where these are non-vanishing, they are bijective. Moreover, since their supports cover , not all of them vanish on and . Therefore and must be the same.
Hence we have an injective immersion. With this prop. says that it is now sufficient to show that we also have a closed map. But this follows generally since is a compact topological space by assumption, and since Euclidean metric space is a Hausdorff topological space (example ), and since maps from compact spaces to Hausdorff spaces are closed and proper (prop. ).
Remark
The Whitney embedding theorem (which we do not prove here) strengthens the statement of prop. in two ways:
-
it applies to non-compact smooth manifolds with a countable set of connected components;
-
it gives the upper bound of on the dimension of the ambient Euclidean space (for embedding of -dimensional manifolds) which turns out to be the minimal ambient dimension such that all -manifolds have an embedding.
This concludes Section 1 Point-set topology.
For the next section see Section 2 – Basic homotopy theory.
References
General
A canonical compendium is
- Nicolas Bourbaki, chapter 1 Topological Structures in Elements of Mathematics III: General topology, Springer (1971, 1990)
Introductory textbooks include
-
John KelleyGeneral Topology, Graduate Texts in Mathematics, Springer (1955)
-
James Munkres, Topology, Prentice Hall (1975, 2000)
Lecture notes include
- Friedhelm Waldhausen, Topologie (pdf)
See also the references at algebraic topology.
Special topics
The standard literature typically omits the following important topics:
Discussion of sober topological spaces is briefly in
- Peter Johnstone, section II 1. of Stone Spaces, Cambridge Studies in Advanced Mathematics 3, Cambridge University Press 1982. xxi+370 pp. MR85f:54002, reprinted 1986.
An introductory textbook that takes sober spaces, and their relation to logic, as the starting point for toplogy is
- Steven Vickers, Topology via Logic, Cambridge University Press (1989)
Detailed discussion of the Hausdorff reflection is in
- Bart van Munster, The Hausdorff quotient, 2014 (pdf)
Index
topology (point-set topology, point-free topology)
see also differential topology, algebraic topology, functional analysis and topological homotopy theory
Basic concepts
-
fiber space, space attachment
Extra stuff, structure, properties
-
Kolmogorov space, Hausdorff space, regular space, normal space
-
sequentially compact, countably compact, locally compact, sigma-compact, paracompact, countably paracompact, strongly compact
Examples
Basic statements
-
closed subspaces of compact Hausdorff spaces are equivalently compact subspaces
-
open subspaces of compact Hausdorff spaces are locally compact
-
compact spaces equivalently have converging subnet of every net
-
continuous metric space valued function on compact metric space is uniformly continuous
-
paracompact Hausdorff spaces equivalently admit subordinate partitions of unity
-
injective proper maps to locally compact spaces are equivalently the closed embeddings
-
locally compact and second-countable spaces are sigma-compact
Theorems
Analysis Theorems
Last revised on June 23, 2024 at 01:05:58. See the history of this page for a list of all contributions to it.